GAMES101-现代计算机图形学入门-闫令琪(1-5) 课程学习笔记
第一节 引入
怎么判断一个游戏画面的技术水平,有一个很简单的方法就是画面亮不亮。
第二节 线性代数
向量
向量是带有方向的量
重要的两个量是方向和长度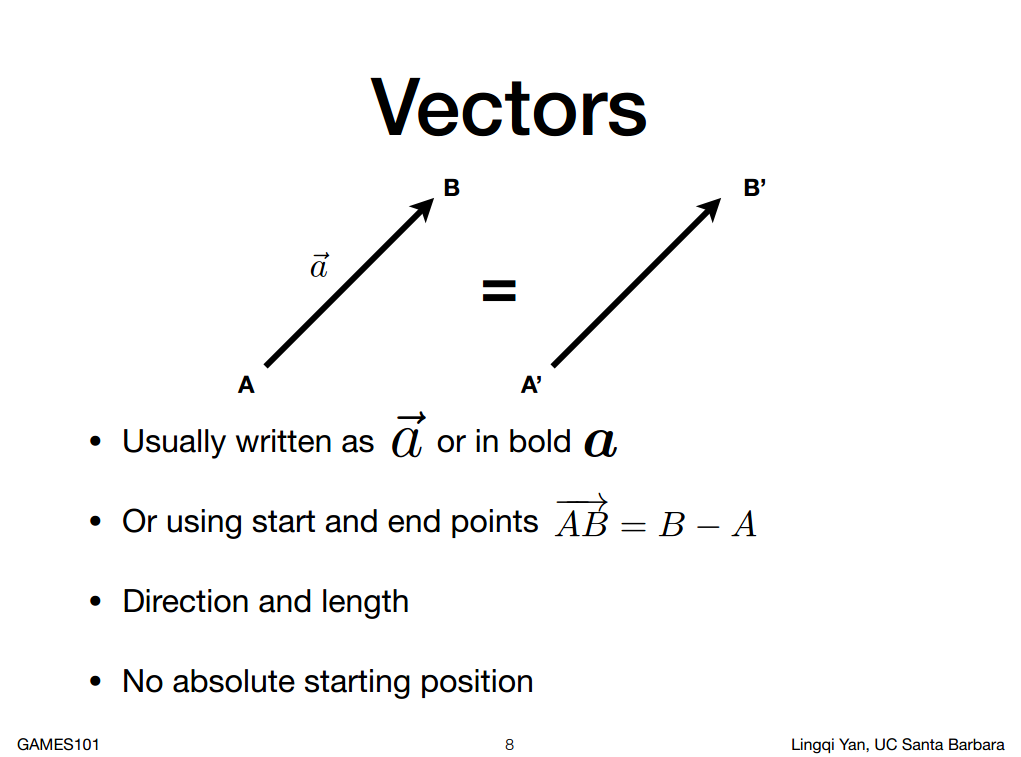
数学: 向量
物理: 矢量
向量长度:
向量加法(求和):
几何上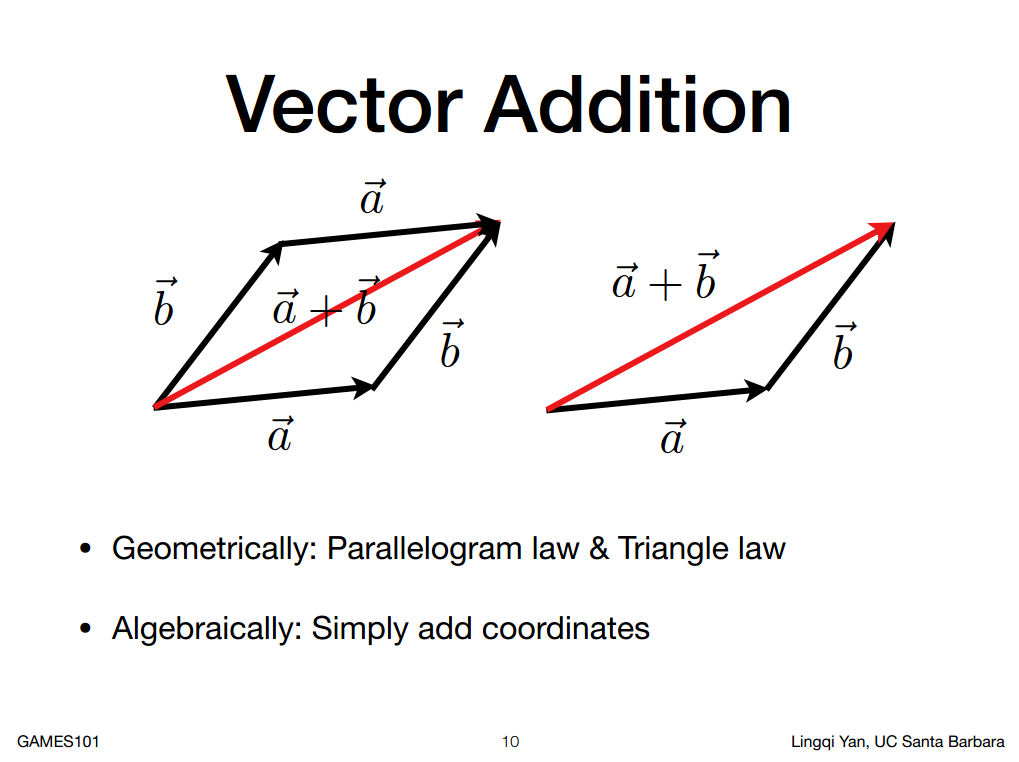
数学上
我们把向量表示成直角坐标系这种形式是有助于计算向量的长度的。
向量的点乘和叉乘
向量更广泛的用法
点乘
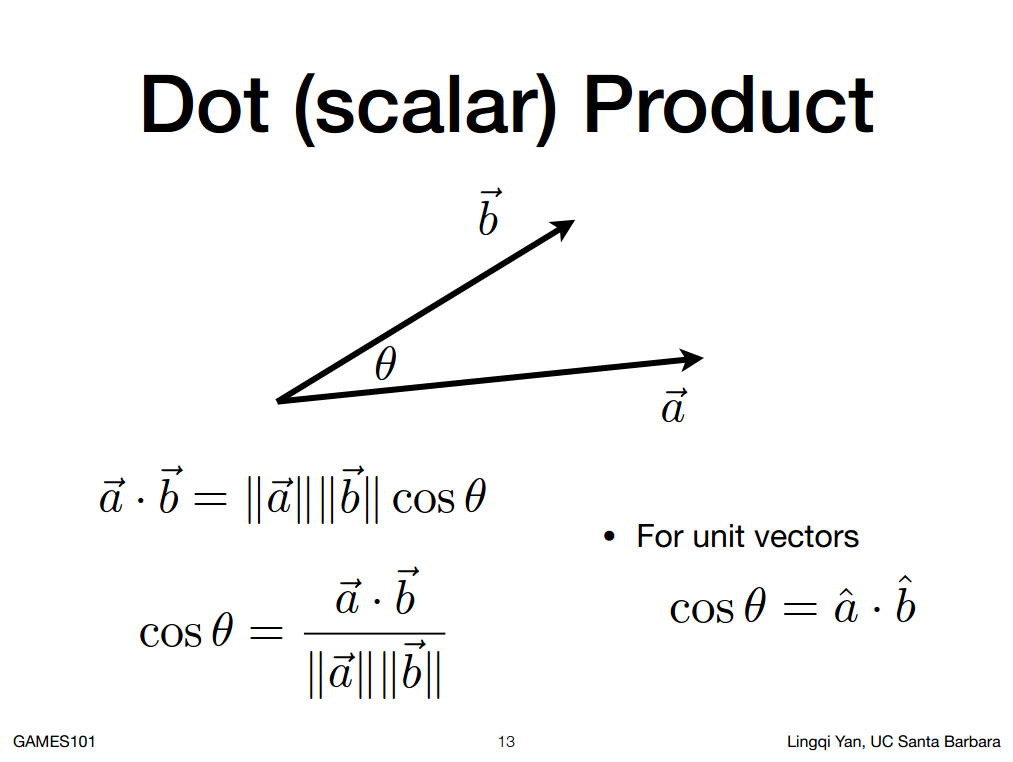 左边是两个向量,右边是一个数字。
如果两个向量都是单位向量,那么它们点乘的结果就是余弦的值。
左边是两个向量,右边是一个数字。
如果两个向量都是单位向量,那么它们点乘的结果就是余弦的值。
 点乘既然是一种运算,运算法则都会满足一些性质。
交换律 结合律 分配律
点乘既然是一种运算,运算法则都会满足一些性质。
交换律 结合律 分配律
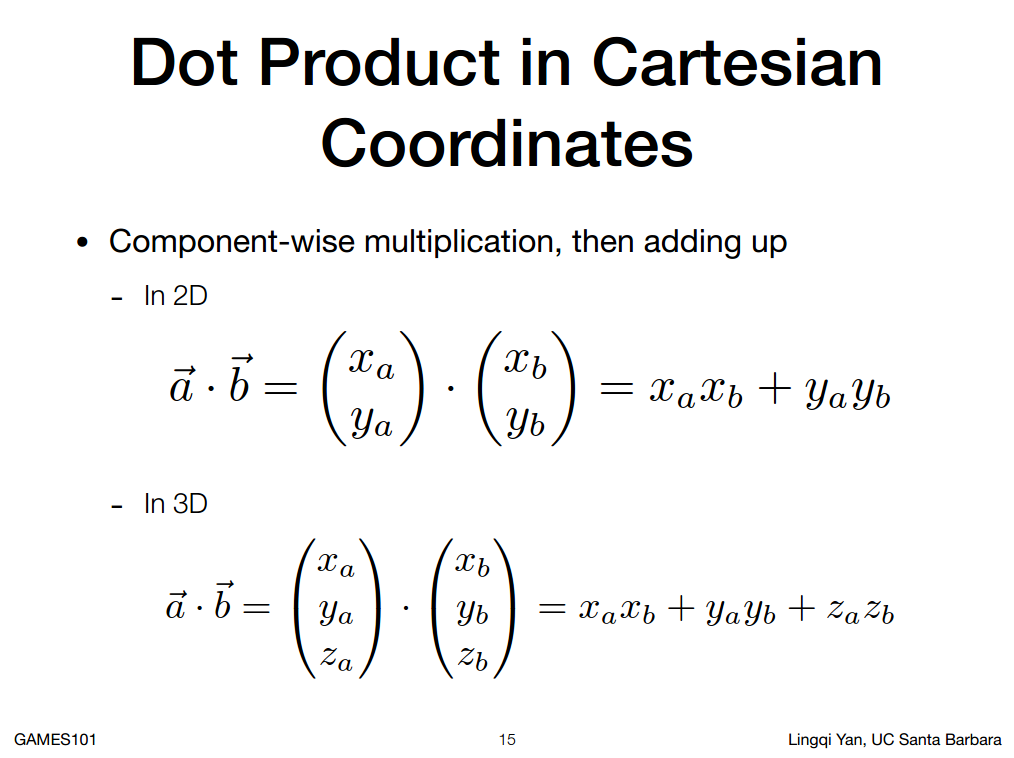 如果是在坐标系下,就跟简单。
如果是在坐标系下,就跟简单。
 1. 点乘在图形学最重要的作用就是找到两个向量的夹角。
比如 光从哪个地方射过来(向量)物体表面法线是什么样的(向量)我们从哪里看(向量)
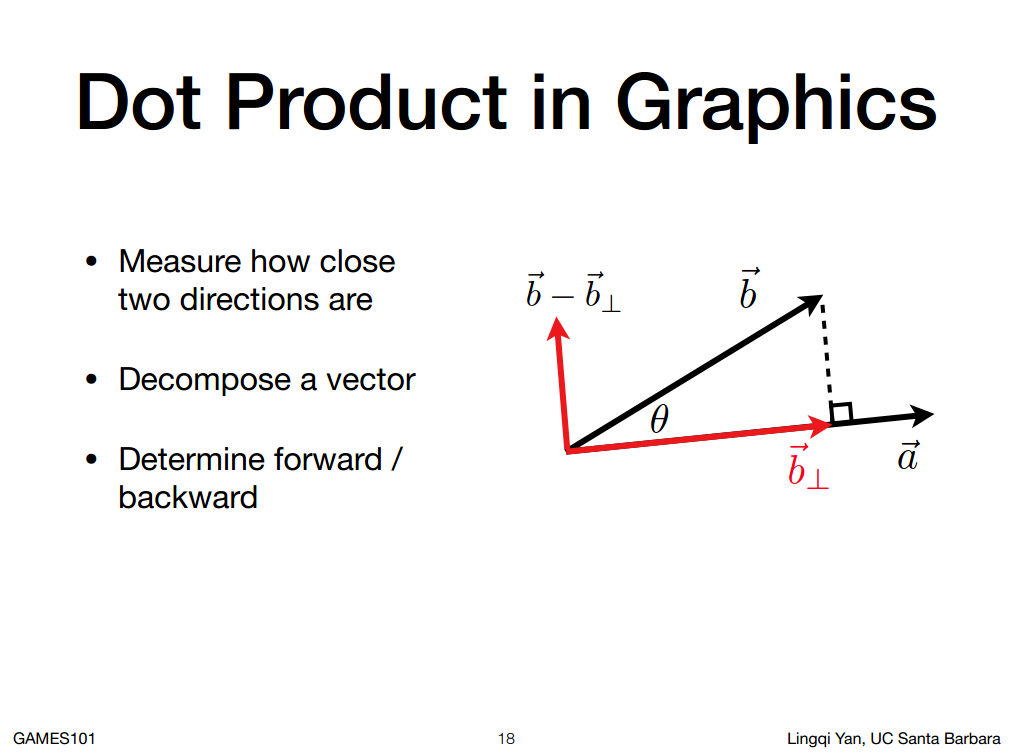
2. 第二个重要作用就是找到一个向量的投影到另一个向量是长什么样的。
投影算出来有什么好处呢? 我们可以把一个向量分解成两个向量,一个平行一个垂直。这样可以帮助我们把任意向量分解到任意坐标轴。
1. 点乘在图形学最重要的作用就是找到两个向量的夹角。
比如 光从哪个地方射过来(向量)物体表面法线是什么样的(向量)我们从哪里看(向量)
2. 第二个重要作用就是找到一个向量的投影到另一个向量是长什么样的。
投影算出来有什么好处呢? 我们可以把一个向量分解成两个向量,一个平行一个垂直。这样可以帮助我们把任意向量分解到任意坐标轴。
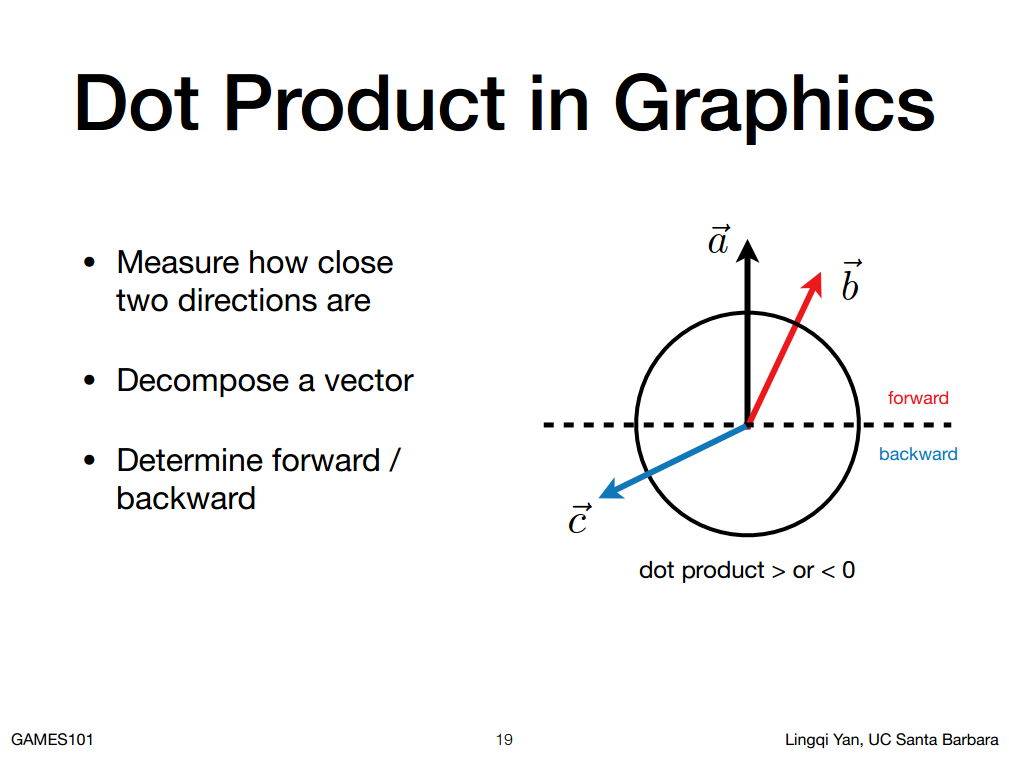
 3. 在图形学里,我们还可以根据点乘的结果判定两个向量是否接近是否远离。
4. 向量点乘还可以告诉大家一个前与后的信息,如图(向量a和向量b点乘为正值且接近1,向量a和向量c点乘为负值,如果有一个向量跟向量a一样,那点乘结果为1,如果有一个向量正好在虚线上,那点乘的值为0,如果跟向量a正好相反,那点乘结果为-1)
3. 在图形学里,我们还可以根据点乘的结果判定两个向量是否接近是否远离。
4. 向量点乘还可以告诉大家一个前与后的信息,如图(向量a和向量b点乘为正值且接近1,向量a和向量c点乘为负值,如果有一个向量跟向量a一样,那点乘结果为1,如果有一个向量正好在虚线上,那点乘的值为0,如果跟向量a正好相反,那点乘结果为-1)
叉乘(叉积)
叉乘是给定两个向量计算出同时垂直与这两个向量的新的向量,另外同时垂直这两个向量也就是必然垂直这两个向量形成的平面
右手螺旋定则(DirectX是右手,openGL是左手)。
定义,右手伸值大拇指向天空,四个拇指朝向手心握(逆时针运动),如果大拇指向大地,四个拇指朝向手心握(顺时针运动)。这里右手指向天空为正,所以逆时针运动为正。
例子:
- Z叉乘X,XYZXYZ,Z到X就是顺时针,所以得到正Y。
- Y叉乘X,XYZXYZ,Y到X就是逆时针,所以得到负Z。
向量的叉乘并不满足交换律(如果要交换需要加一个负号)
向量的叉积还有一个作用是我们利用它来建立一个三维空间中的直角坐标系
几何:
叉积怎么算,有什么用处: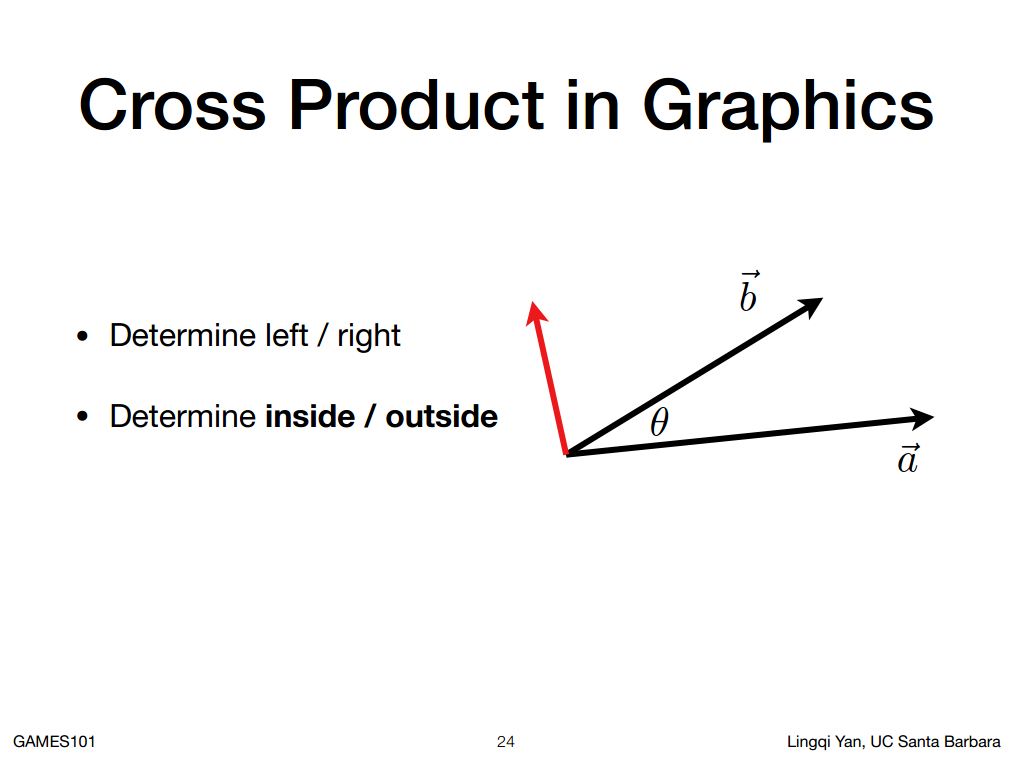
特别重要
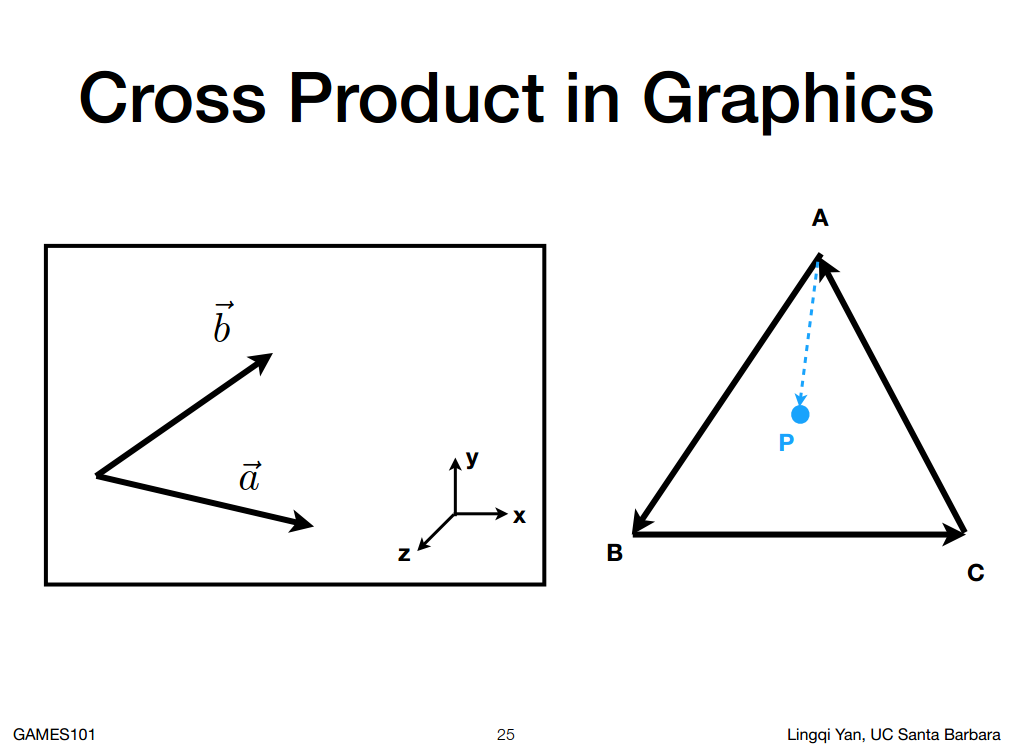 1. 判定左和右
如图左侧,XY为平面,通过右手螺旋定则,Z为朝向我们自身的向量,如果想判断向量b在向量a左侧还是右侧(什么是左侧右侧? 从向量a顺时针旋转到达向量b为左侧,逆时针为右侧),在这里根据图示很容易看出来向量b是在向量a的左侧,如果用数字表示就是 向量a叉乘向量b得到的结果是正值(指向身体)就说明向量b在向量a的左侧,如果向量b叉乘向量a得到的结果是负值(指向身体外侧),那就说明向量a在向量b右侧,
2. 判定内与外
如图右侧,先判断向量AP是否在向量AB的左侧,在判断向量BP是否在向量BC的左侧,在判断向量AP是否在ac的左侧,如果都是在左侧就说明点P在三角形内部,否则肯定有一个判断是在右侧。
这里假设了ABC三个点是逆时针排布,如果换成顺时针也没有问题,只不过是都在左侧。
所以我们可以忽略三角形的排布顺序,只要三个边左或者右保持一致就说明点在三角形内部。这点非常重要,是光栅化的基础(用来判断像素是否在三角形的内部)。
1. 判定左和右
如图左侧,XY为平面,通过右手螺旋定则,Z为朝向我们自身的向量,如果想判断向量b在向量a左侧还是右侧(什么是左侧右侧? 从向量a顺时针旋转到达向量b为左侧,逆时针为右侧),在这里根据图示很容易看出来向量b是在向量a的左侧,如果用数字表示就是 向量a叉乘向量b得到的结果是正值(指向身体)就说明向量b在向量a的左侧,如果向量b叉乘向量a得到的结果是负值(指向身体外侧),那就说明向量a在向量b右侧,
2. 判定内与外
如图右侧,先判断向量AP是否在向量AB的左侧,在判断向量BP是否在向量BC的左侧,在判断向量AP是否在ac的左侧,如果都是在左侧就说明点P在三角形内部,否则肯定有一个判断是在右侧。
这里假设了ABC三个点是逆时针排布,如果换成顺时针也没有问题,只不过是都在左侧。
所以我们可以忽略三角形的排布顺序,只要三个边左或者右保持一致就说明点在三角形内部。这点非常重要,是光栅化的基础(用来判断像素是否在三角形的内部)。
向量定义坐标系
 向量叉乘可以定义一些互相垂直的轴,就会形成坐标系如图。
向量叉乘可以定义一些互相垂直的轴,就会形成坐标系如图。
 这里顶一个uvw坐标系,三个向量单位长度都为1,互相垂直,给你u和v 叉乘得到w。
我们可以利用投影把任意一个向量分解到三个轴上去,利用点乘,因为什么呢?向量P点乘向量U,等于是向量P的长度乘以向量U的长度在乘以cosθ,向量U又恰好是单位向量为1,等于是向量P的长度乘以cosθ,根据下图三角函数,就会得出向量P在向量U上的投影,同理获得向量P在向量V和向量W上的投影,有了这三个投影就可以获得坐标系下的这个向量。
这里顶一个uvw坐标系,三个向量单位长度都为1,互相垂直,给你u和v 叉乘得到w。
我们可以利用投影把任意一个向量分解到三个轴上去,利用点乘,因为什么呢?向量P点乘向量U,等于是向量P的长度乘以向量U的长度在乘以cosθ,向量U又恰好是单位向量为1,等于是向量P的长度乘以cosθ,根据下图三角函数,就会得出向量P在向量U上的投影,同理获得向量P在向量V和向量W上的投影,有了这三个投影就可以获得坐标系下的这个向量。
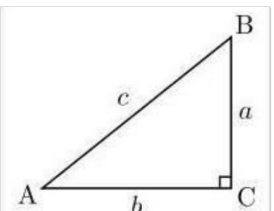 cosA = c/b
cosA = c/b
矩阵
 **在图像学里,变换就是矩阵的最大应用。**
**在图像学里,变换就是矩阵的最大应用。**
 ##### 矩阵乘以和加上一个常量就是把矩阵的每个元素乘以和加上一个常量.
##### 矩阵相乘
##### 矩阵乘以和加上一个常量就是把矩阵的每个元素乘以和加上一个常量.
##### 矩阵相乘
 矩阵乘矩阵必须要符合条件才能乘,如图必须第一个矩阵的列数和第二个矩阵的行数相同相乘才有意义。
**关于新得到的矩阵每一个元素都是什么,有不同的数学定义,这个地方比较不容易记住,这里给大家提供一个容易记得方法,比如左下角这个8,他的坐标是三行一列,这里三行对应第一个矩阵(0,4),一列对应第二个矩阵(3,2),这两个向量点乘。**
矩阵乘矩阵必须要符合条件才能乘,如图必须第一个矩阵的列数和第二个矩阵的行数相同相乘才有意义。
**关于新得到的矩阵每一个元素都是什么,有不同的数学定义,这个地方比较不容易记住,这里给大家提供一个容易记得方法,比如左下角这个8,他的坐标是三行一列,这里三行对应第一个矩阵(0,4),一列对应第二个矩阵(3,2),这两个向量点乘。**
 矩阵乘法是没有交换律的,但是矩阵是由结合律和分配律。
矩阵乘法是没有交换律的,但是矩阵是由结合律和分配律。
矩阵乘向量
 >一个矩阵如何和一个向量乘?当我们认为向量是列向量就有意义了(也就是说M永远为1)。
>一个矩阵如何和一个向量乘?当我们认为向量是列向量就有意义了(也就是说M永远为1)。
这是最重要的核心。
下面表示一个2D向量按Y轴镜像的操作。
矩阵转置
 性质: 如果要乘两个矩阵在转置好比相对后一个矩阵做装置在乘以前一个矩阵做转置的结果。
性质: 如果要乘两个矩阵在转置好比相对后一个矩阵做装置在乘以前一个矩阵做转置的结果。
特殊的矩阵,单位矩阵
 对角阵,只有对角线上有非零的元素,
矩阵的逆:如果你能找到一个矩阵,和原来的矩阵相乘,不管乘得顺序,得到的结果都是I,那么我们就认为这两个矩阵是互逆的。
逆矩阵的计算和转置的矩阵很相似。
对角阵,只有对角线上有非零的元素,
矩阵的逆:如果你能找到一个矩阵,和原来的矩阵相乘,不管乘得顺序,得到的结果都是I,那么我们就认为这两个矩阵是互逆的。
逆矩阵的计算和转置的矩阵很相似。
向量点乘和叉乘的矩阵形式
 点乘:向量a点乘向量b 等于向量a转置和向量b的乘法。
叉乘:相对点乘困难一些,相当于把向量a转换成一个矩阵(dual matrix)乘以向量b
点乘:向量a点乘向量b 等于向量a转置和向量b的乘法。
叉乘:相对点乘困难一些,相当于把向量a转换成一个矩阵(dual matrix)乘以向量b
第三节 变换

 #### 我们为什么要学习变换:
* Modeling:
位移 旋转 缩放
很多动画就是由各种不同的变换合成在一起形成的。
* Viewing:
#### 我们为什么要学习变换:
* Modeling:
位移 旋转 缩放
很多动画就是由各种不同的变换合成在一起形成的。
* Viewing:
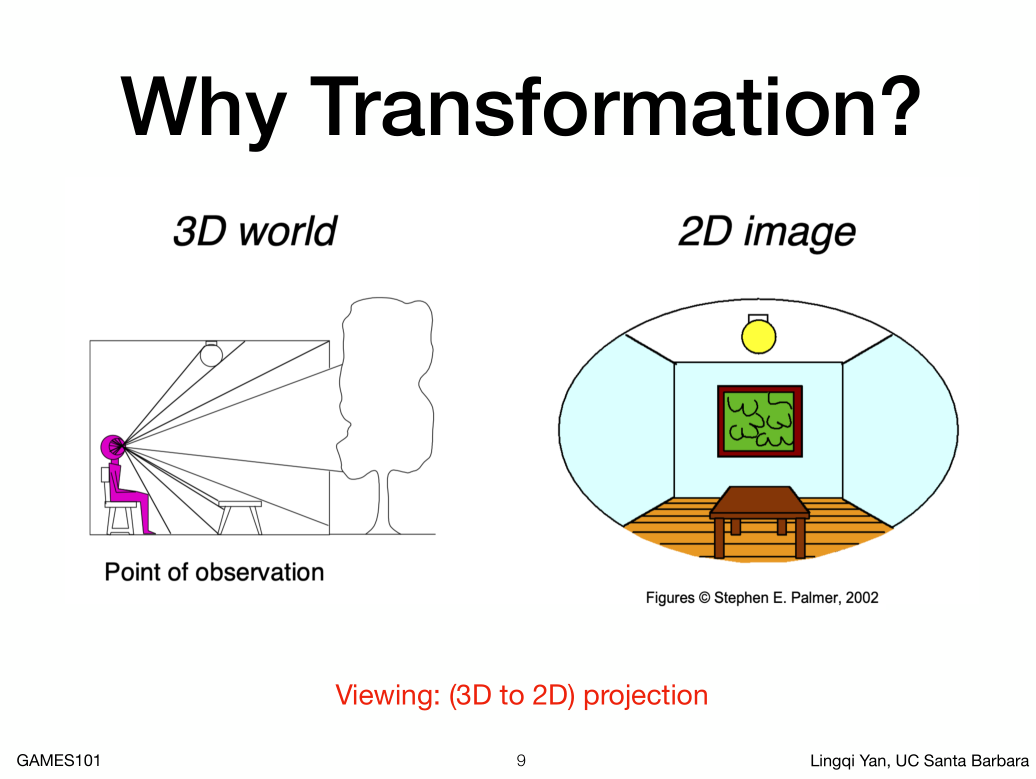 光栅化成像涉及到大量的变换。
3D -> 2D 从三维到二维的变换我们叫做投影,这个投影也是一种非常重要的变换,之后会学到。
#### 变换
光栅化成像涉及到大量的变换。
3D -> 2D 从三维到二维的变换我们叫做投影,这个投影也是一种非常重要的变换,之后会学到。
#### 变换
 今天我们的目标就是,把矩阵和变换联系起来。
#### 例子
##### 标准缩放
今天我们的目标就是,把矩阵和变换联系起来。
#### 例子
##### 标准缩放
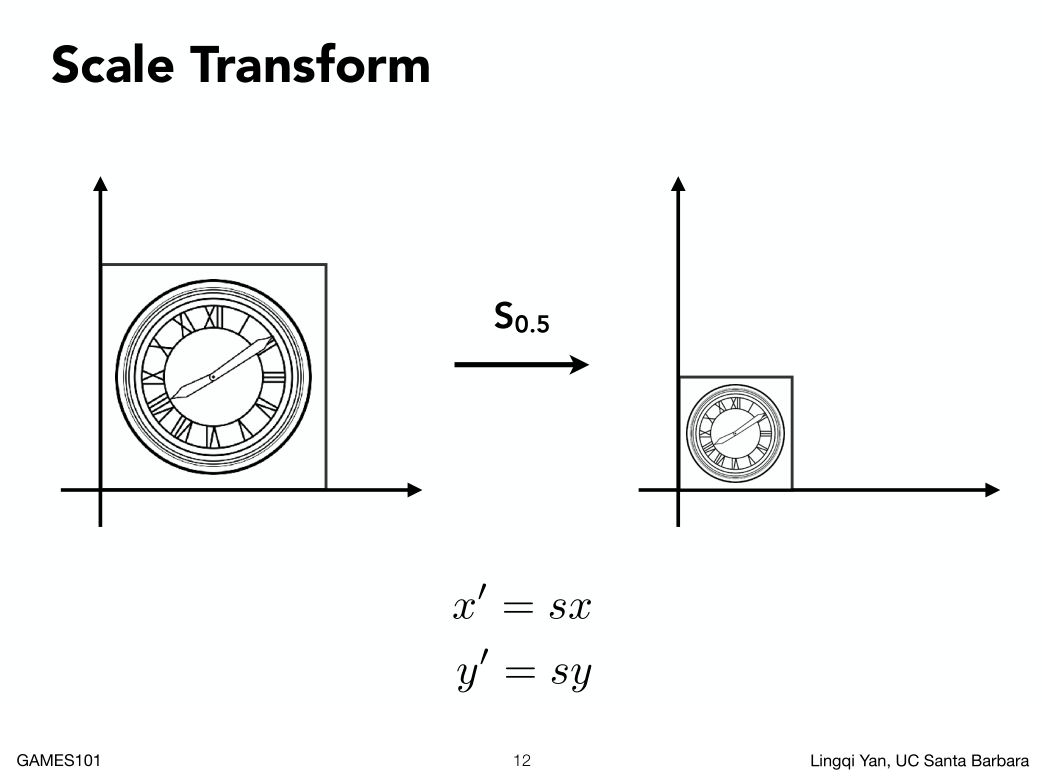 横轴和纵轴都缩放了0.5,也就是说把任何一个点坐标(X,Y)进行缩放操作0.5倍。
如果用数学形式表示, 可以表示为
横轴和纵轴都缩放了0.5,也就是说把任何一个点坐标(X,Y)进行缩放操作0.5倍。
如果用数学形式表示, 可以表示为
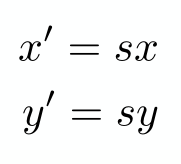 如果用矩阵形式表示可以表示为对角矩阵。
如果用矩阵形式表示可以表示为对角矩阵。
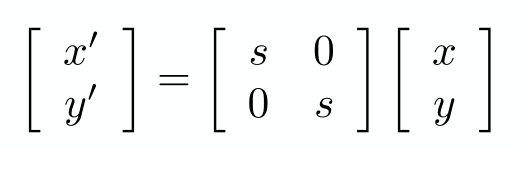 是不是这样的,我们可以验证一下。
是不是这样的,我们可以验证一下。
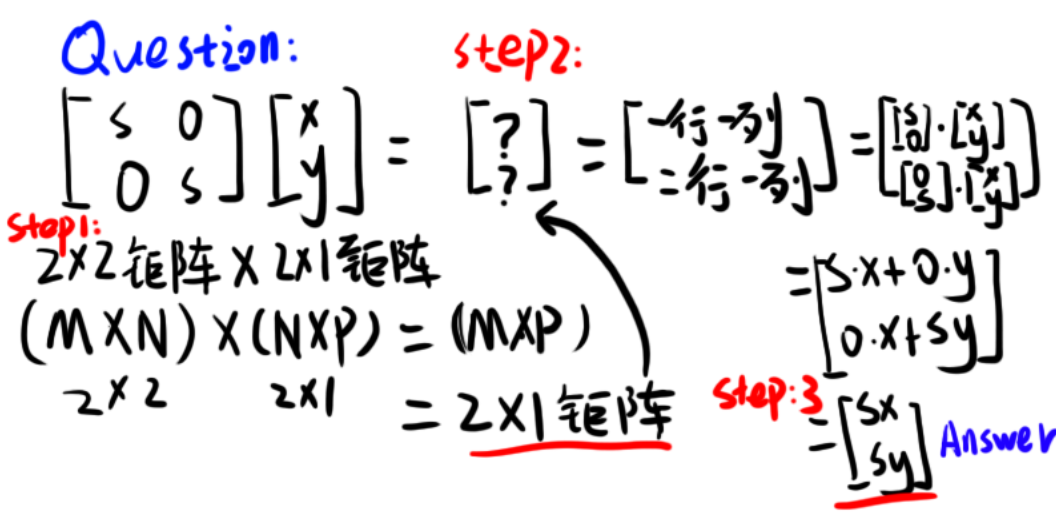 ##### 如果XY的缩放各不相同:
##### 如果XY的缩放各不相同:
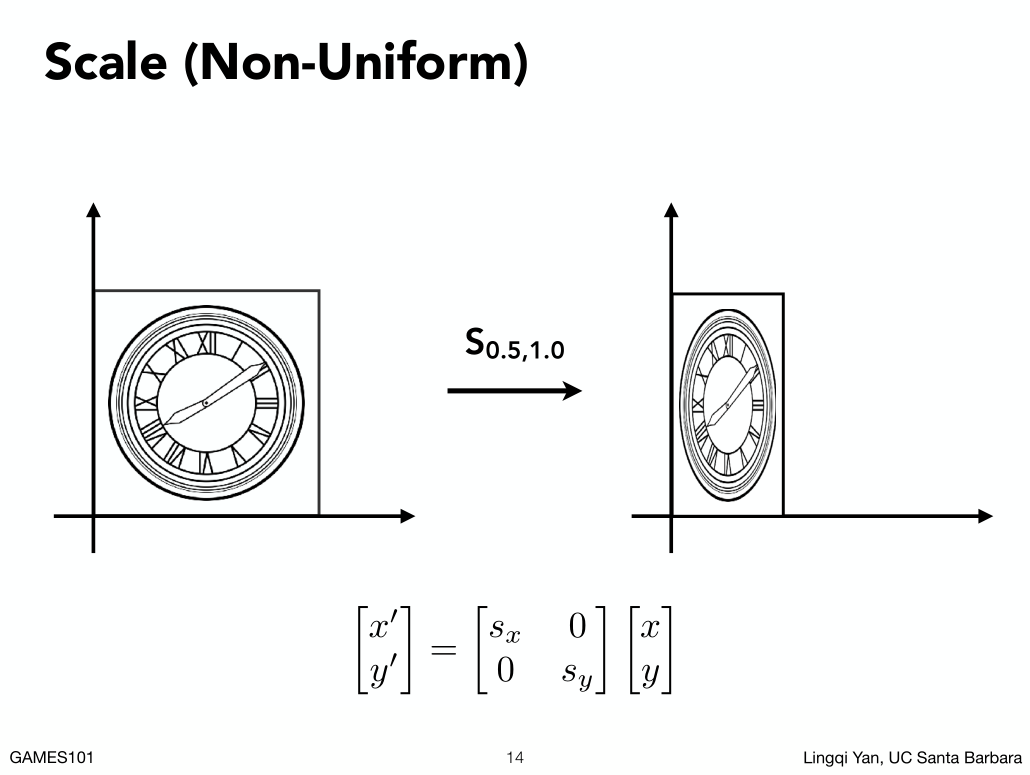 ##### 如果是反射(对称)的操作:
##### 如果是反射(对称)的操作:
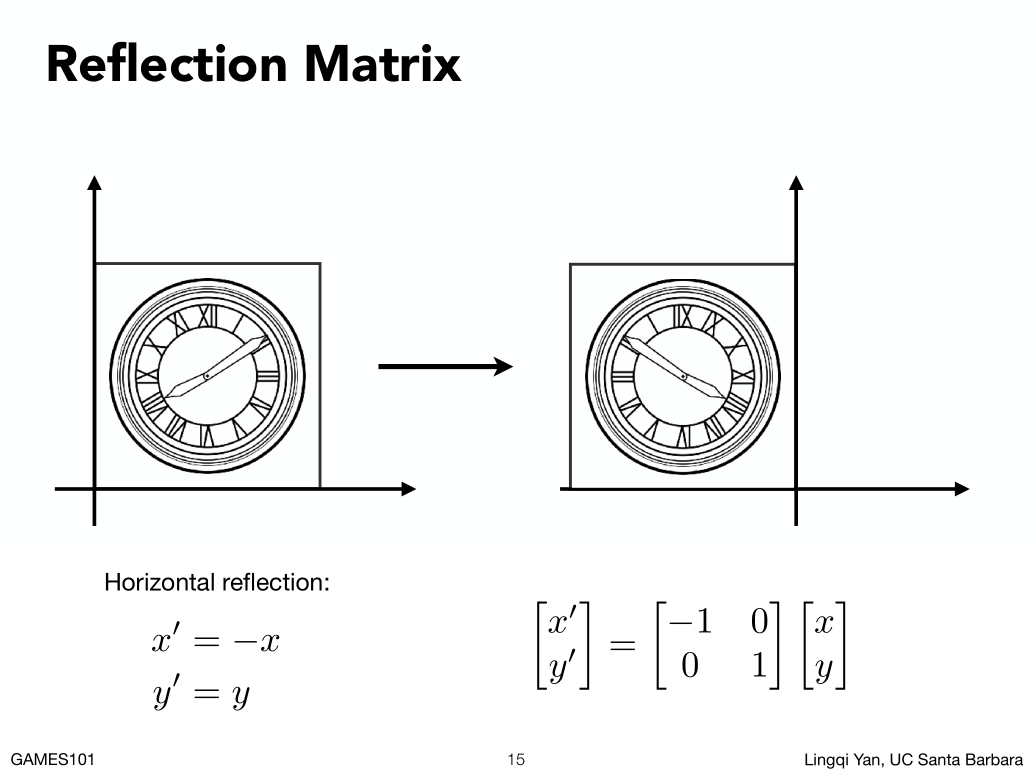 等于是Y轴不变,X轴反过来。
##### 如果是切变的操作:
等于是Y轴不变,X轴反过来。
##### 如果是切变的操作:
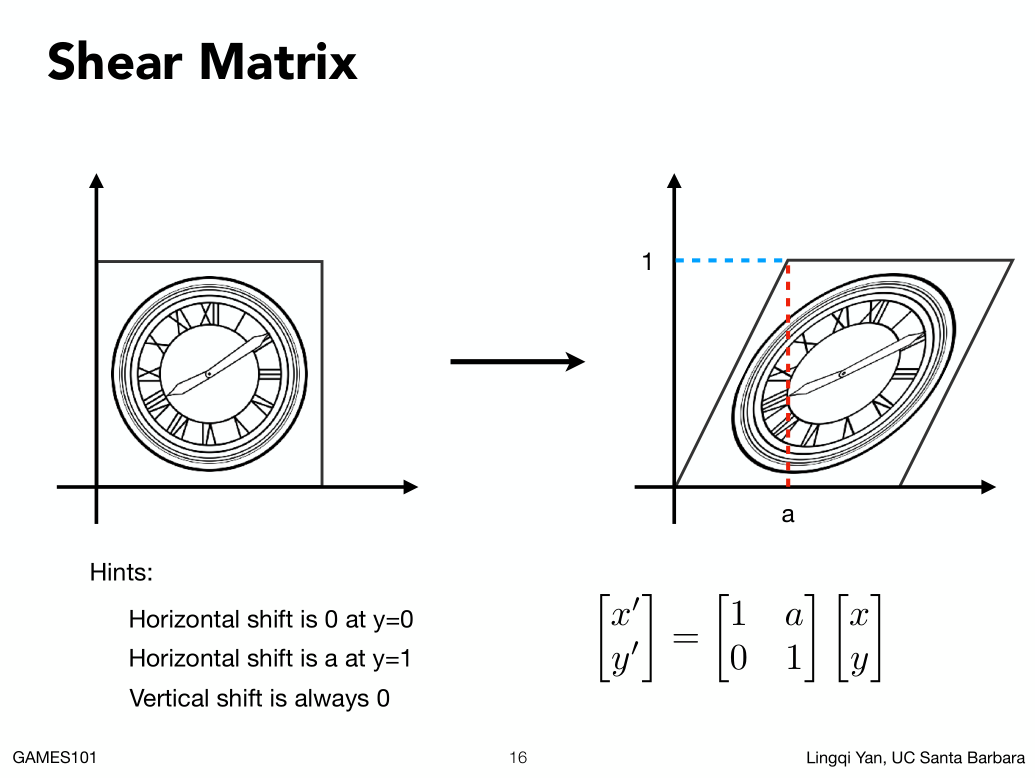 注意这里可以通过一个点的变换前到变换后的变化推导出,Y是不变的,X是变成了X+ay,由x+ay倒推出矩阵.
##### 如果是旋转的操作:
注意这里可以通过一个点的变换前到变换后的变化推导出,Y是不变的,X是变成了X+ay,由x+ay倒推出矩阵.
##### 如果是旋转的操作:
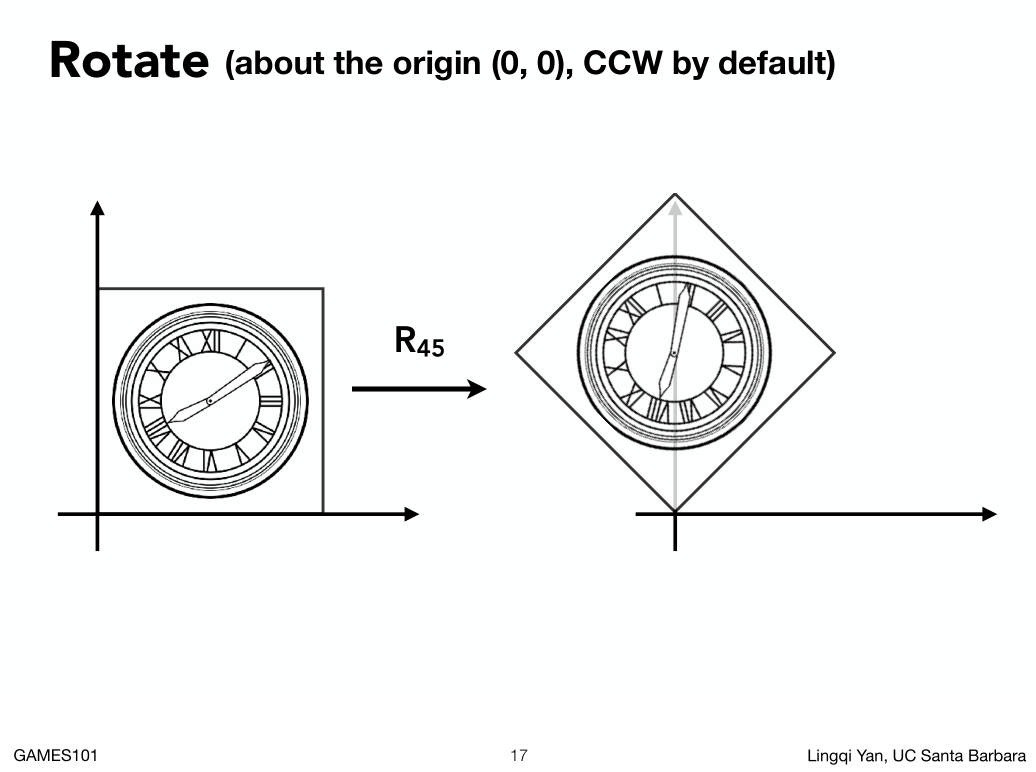 默认是绕(0,0)点旋转,逆时针旋转.
默认是绕(0,0)点旋转,逆时针旋转.
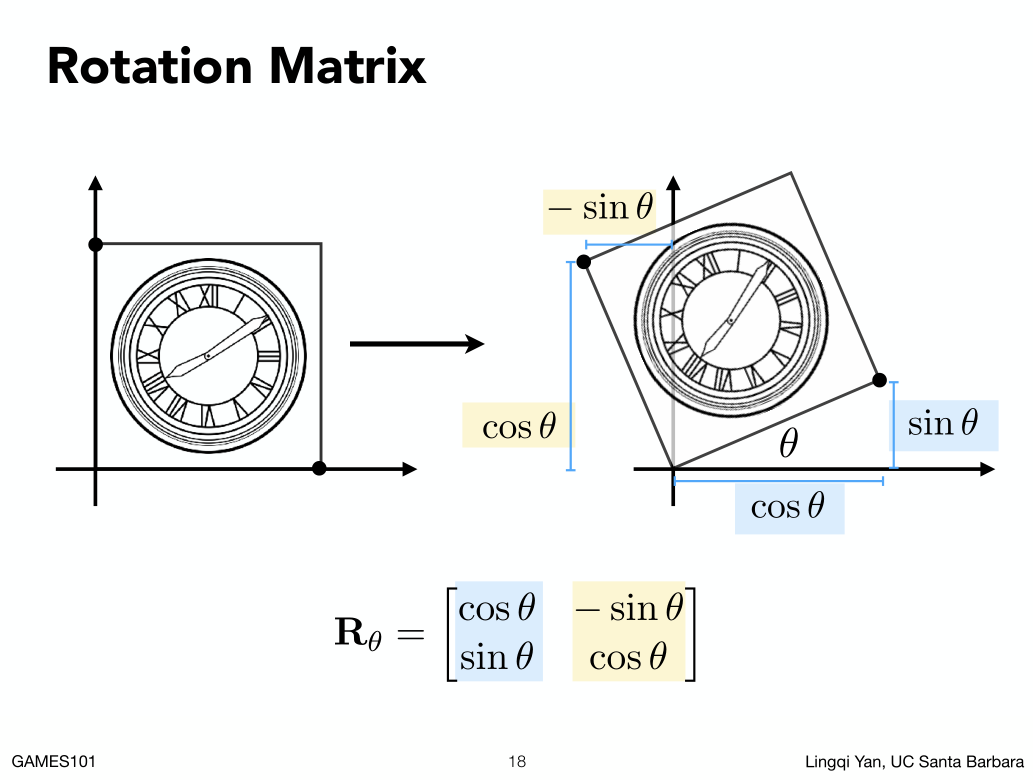 简单的推导:
* 不管再复杂的操作,先找到一个一一对应的关系点,再倒推。
简单的推导:
* 不管再复杂的操作,先找到一个一一对应的关系点,再倒推。
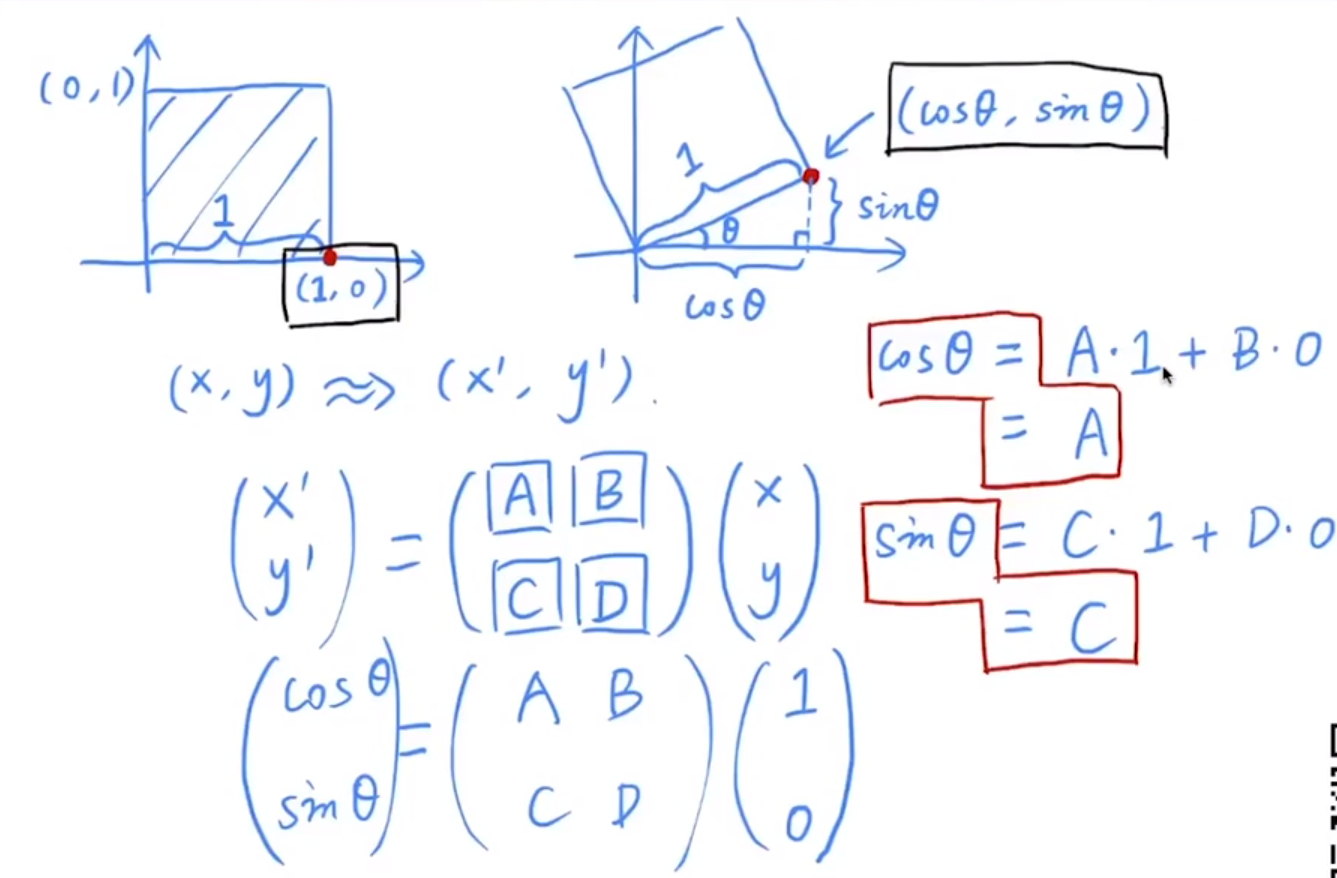 通过(1,0)点的对应关系点配合三角函数可以得到矩阵AC值,那么通过(0,1)点的对应关系点可以找到BC.
##### 变换的共同点
通过(1,0)点的对应关系点配合三角函数可以得到矩阵AC值,那么通过(0,1)点的对应关系点可以找到BC.
##### 变换的共同点
 X pu ruai mu = 变换矩阵*X
这样变换和矩阵的联系就建立起来了,对于一个变换就可以用矩阵来表示。
概念区分: 我们要用一个相同维度的矩阵来乘以向量。
#### 齐次坐标
X pu ruai mu = 变换矩阵*X
这样变换和矩阵的联系就建立起来了,对于一个变换就可以用矩阵来表示。
概念区分: 我们要用一个相同维度的矩阵来乘以向量。
#### 齐次坐标
为什么要学习齐次坐标,为什么要引入这个复杂的东西。
因为平移变换特别特殊。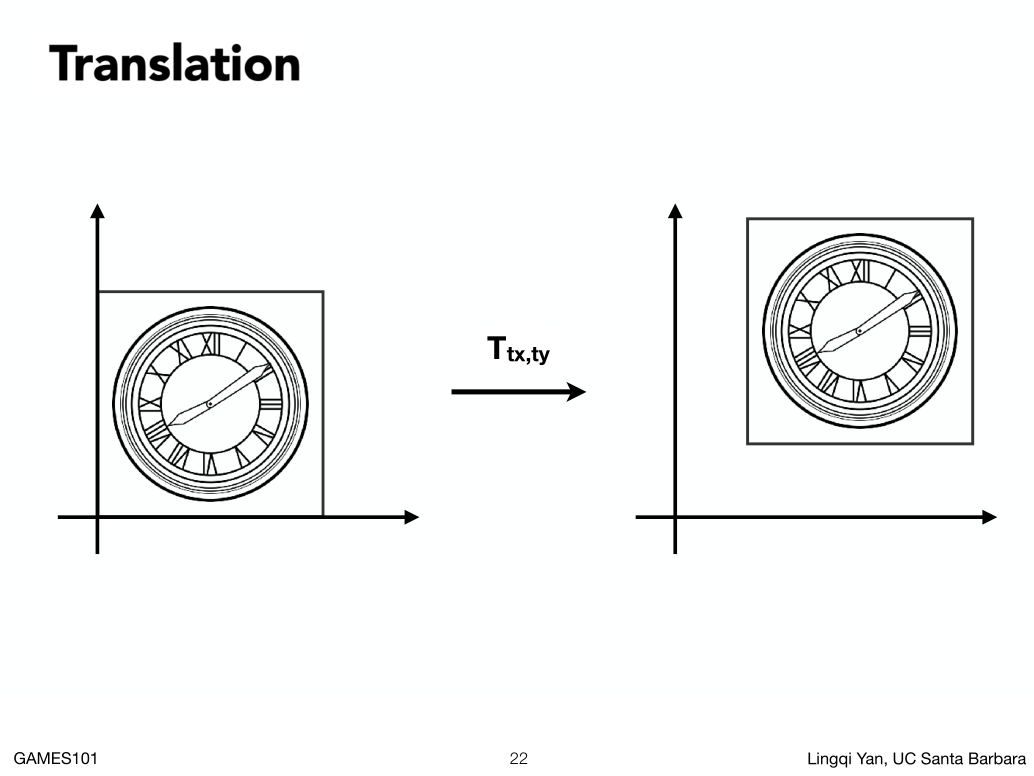
如果简单的写出来,是挺简单的,但是没有办法转换成矩阵: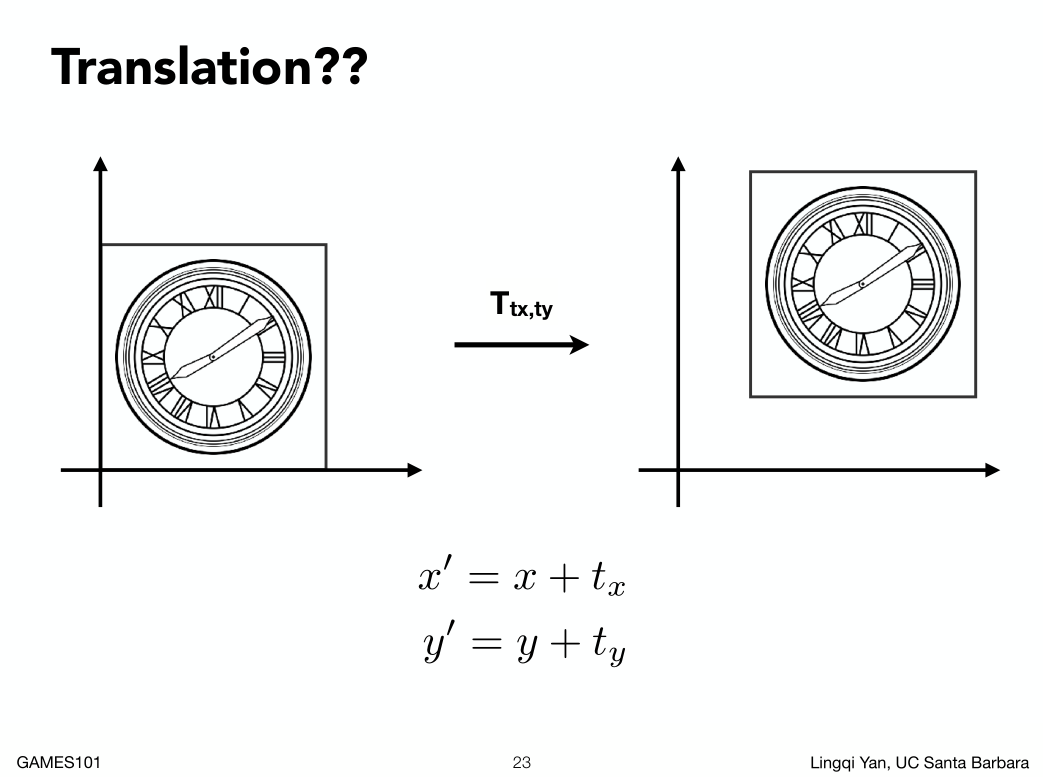
所以无奈之下必须要用齐次坐标。
平移操作并不属于一个线性变换(因为线性变换必须等于一个向量等于一个矩阵乘以另外一个向量),但是我们不希望把平移当作一个特殊的情况处理,因为人类总是懒的。所以有没有办法可以把我们提到的所有变换归纳成一个最简单的变换来表示。
tradeoff:权衡.
齐次坐标
 如果XY表示点的坐标那就加上1,如果是向量加上0。为什么区别对待?
因为向量具有**平移不变性**:
如果有一个向量经过一个表示平移的矩阵,我们希望它的结果还是XY0.
>向量是个所谓的“过程量”,不依赖于本身的位置。
如果XY表示点的坐标那就加上1,如果是向量加上0。为什么区别对待?
因为向量具有**平移不变性**:
如果有一个向量经过一个表示平移的矩阵,我们希望它的结果还是XY0.
>向量是个所谓的“过程量”,不依赖于本身的位置。
 1. 如果两个向量相加,结果是新的向量(x1+x2,y1+y2,0+0)有意义。
2. 如果两个点相减(形成一个从被减数指向减数向量)(x1-x2,y1-y2,1-1=0)点减点等于向量,有意义。
3. 如果是点加向量,一个点沿着向量移动到一个新的点上,
(x1+x2,y1+y2,1+0=1)有意义。
4. 一个点加一个点,没意义,扩充的定义。
5. 对于任何的二维点,我们认为,(x/w,y/2,w/w),w!=0(0就是向量了。)
6. 一个点加一个点,表示这两个点的中点。为什么?因为一个点加一个点w会变成2,这个w变成1的过程就是在求中点。
1. 如果两个向量相加,结果是新的向量(x1+x2,y1+y2,0+0)有意义。
2. 如果两个点相减(形成一个从被减数指向减数向量)(x1-x2,y1-y2,1-1=0)点减点等于向量,有意义。
3. 如果是点加向量,一个点沿着向量移动到一个新的点上,
(x1+x2,y1+y2,1+0=1)有意义。
4. 一个点加一个点,没意义,扩充的定义。
5. 对于任何的二维点,我们认为,(x/w,y/2,w/w),w!=0(0就是向量了。)
6. 一个点加一个点,表示这两个点的中点。为什么?因为一个点加一个点w会变成2,这个w变成1的过程就是在求中点。
最重要的不是这些变换,而是目的,我们的目的是就是为了把所有的变换写出一个矩阵乘以一个向量的形式。
仿射变换
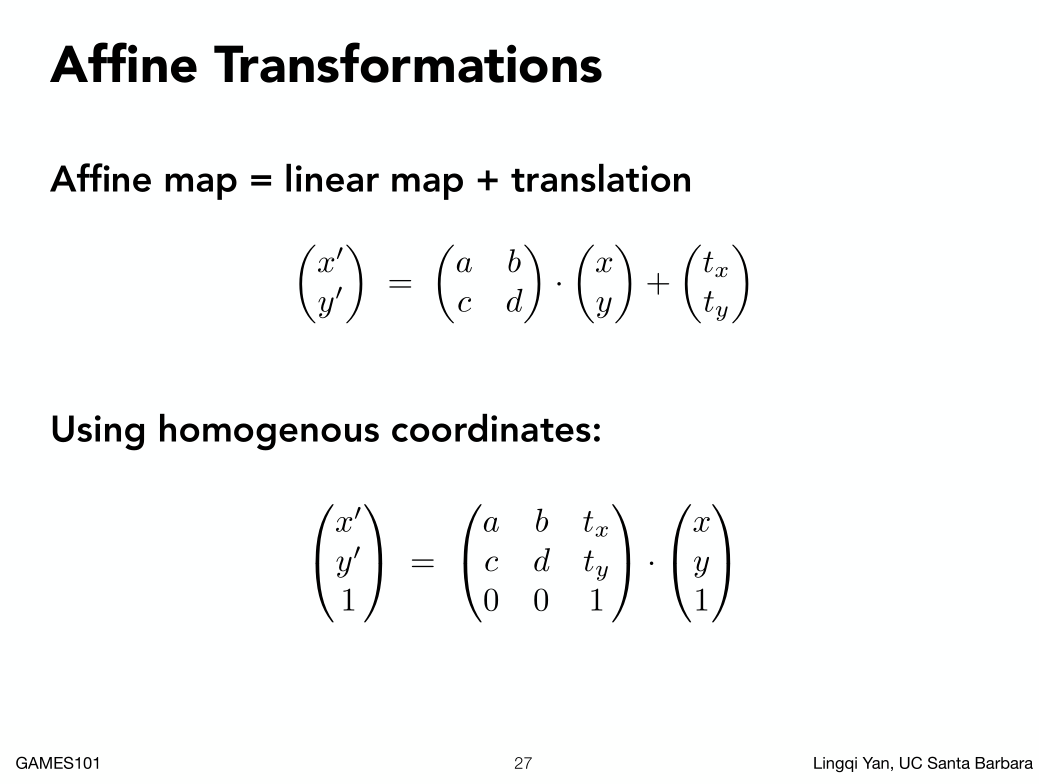 线性变换+位移,对于类似的变换就叫仿射变换。
所有的仿射变换都可以写成齐次坐标这种形式。
验证:
线性变换+位移,对于类似的变换就叫仿射变换。
所有的仿射变换都可以写成齐次坐标这种形式。
验证:
 只要表示**仿射变换**最后一行都是001,理论上只用存储上面的部分就行了。
##### 逆变换
逆变换是指把一个变换的操作反过来。
在数学对应的正好是乘以这个变换的逆矩阵(一个矩阵乘以它自己的逆矩阵一定等于单位矩阵)
只要表示**仿射变换**最后一行都是001,理论上只用存储上面的部分就行了。
##### 逆变换
逆变换是指把一个变换的操作反过来。
在数学对应的正好是乘以这个变换的逆矩阵(一个矩阵乘以它自己的逆矩阵一定等于单位矩阵)
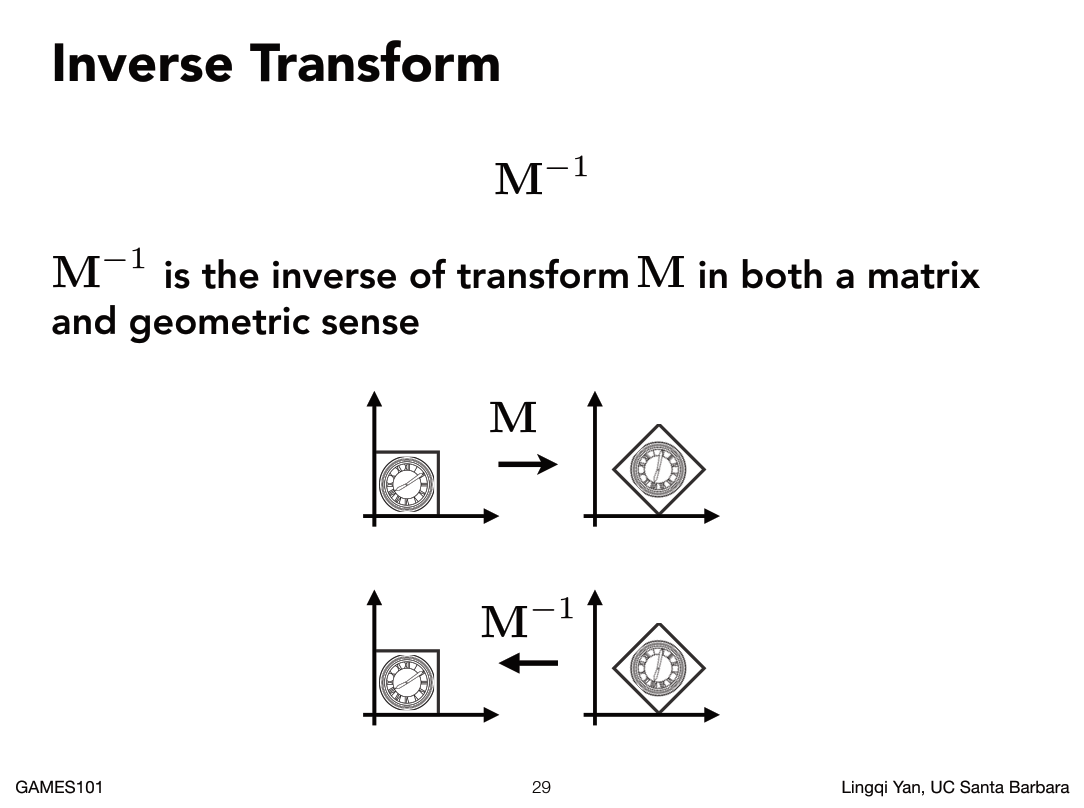
变换组合/分解
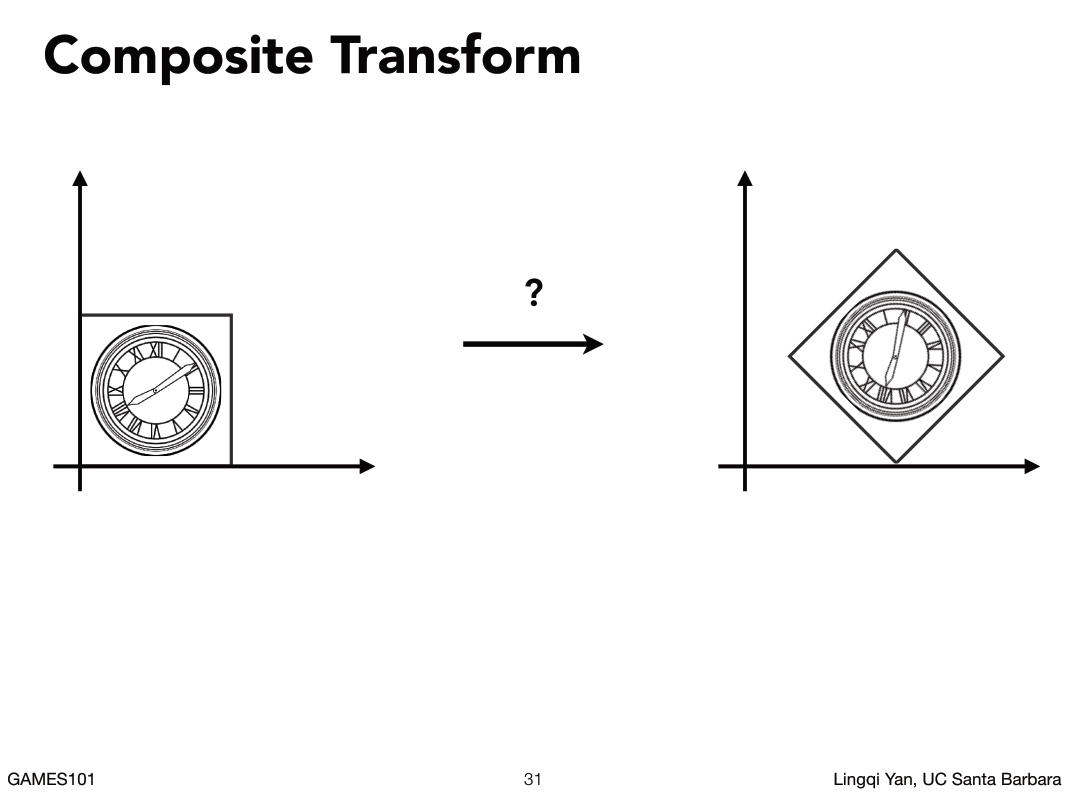 对于这样一个变换我们可以把它看成先平移在旋转,如下图:
对于这样一个变换我们可以把它看成先平移在旋转,如下图:
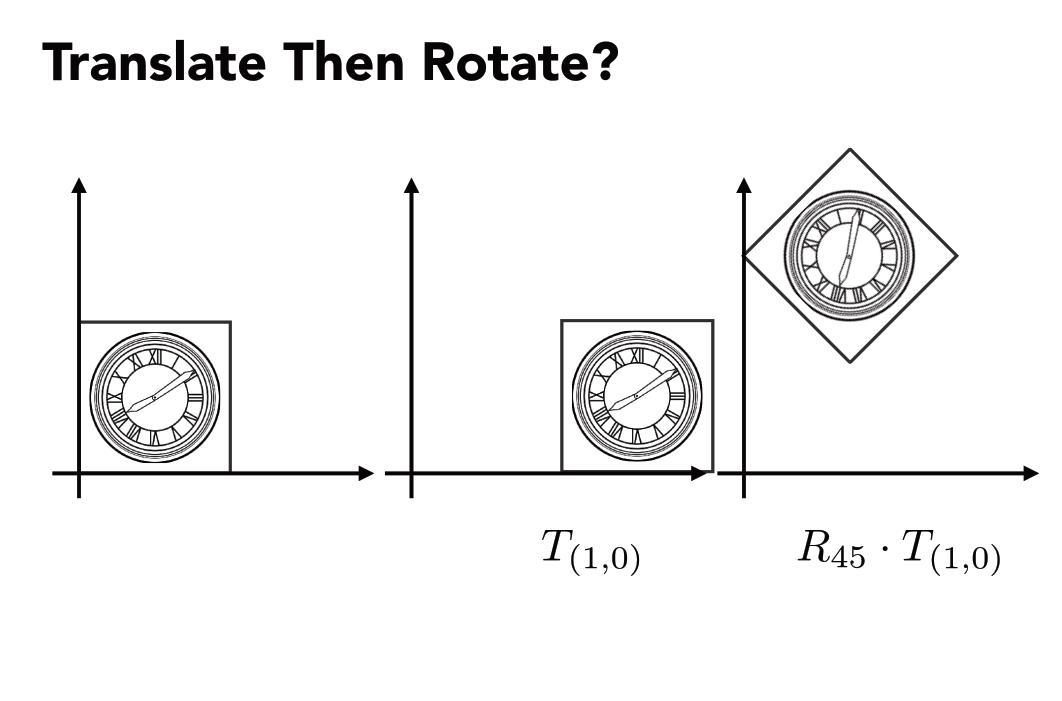 但是结果不对,因为旋转还是绕(0,0)点。怎么操作对呢?如下图:
但是结果不对,因为旋转还是绕(0,0)点。怎么操作对呢?如下图:
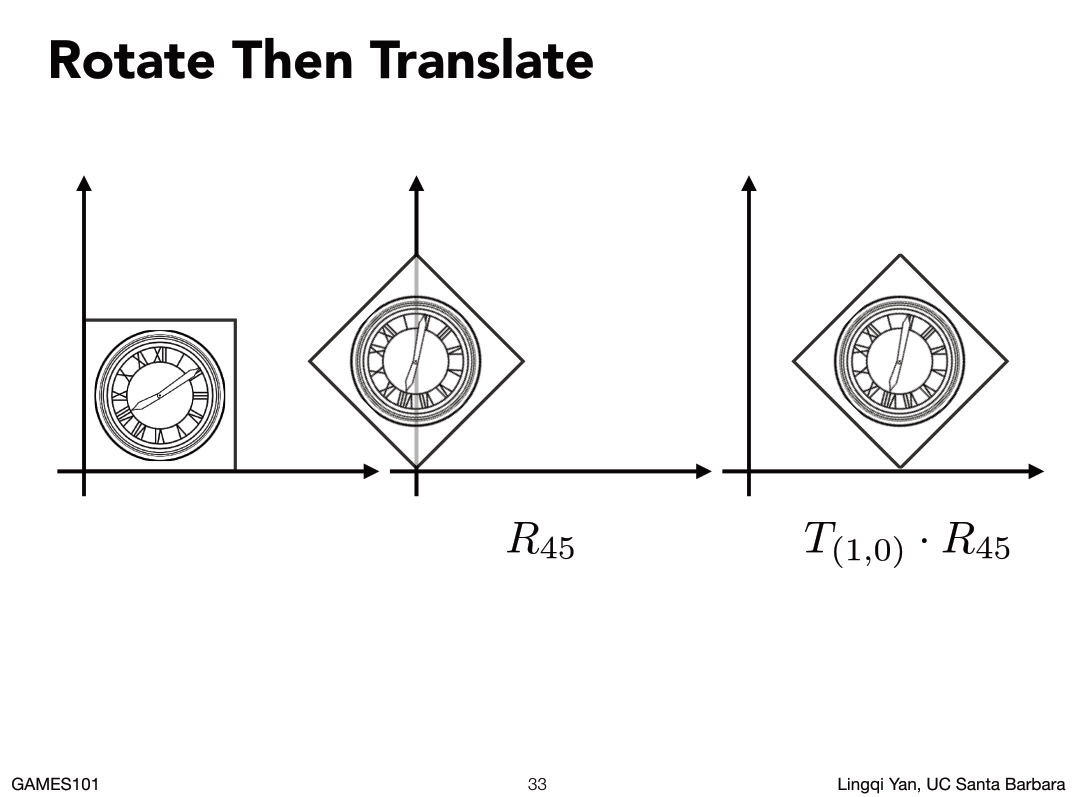
如此可以得到两个信息:
- 复杂的变换可以通过简单的变化得到。
- 变换的顺序非常重要。(对应矩阵乘法不满足交换律{变换就是在某一个向量前面乘以一个矩阵,再变换一次就是再在前面乘以一个矩阵,矩阵的乘的顺序变换那结果就会发生变化})
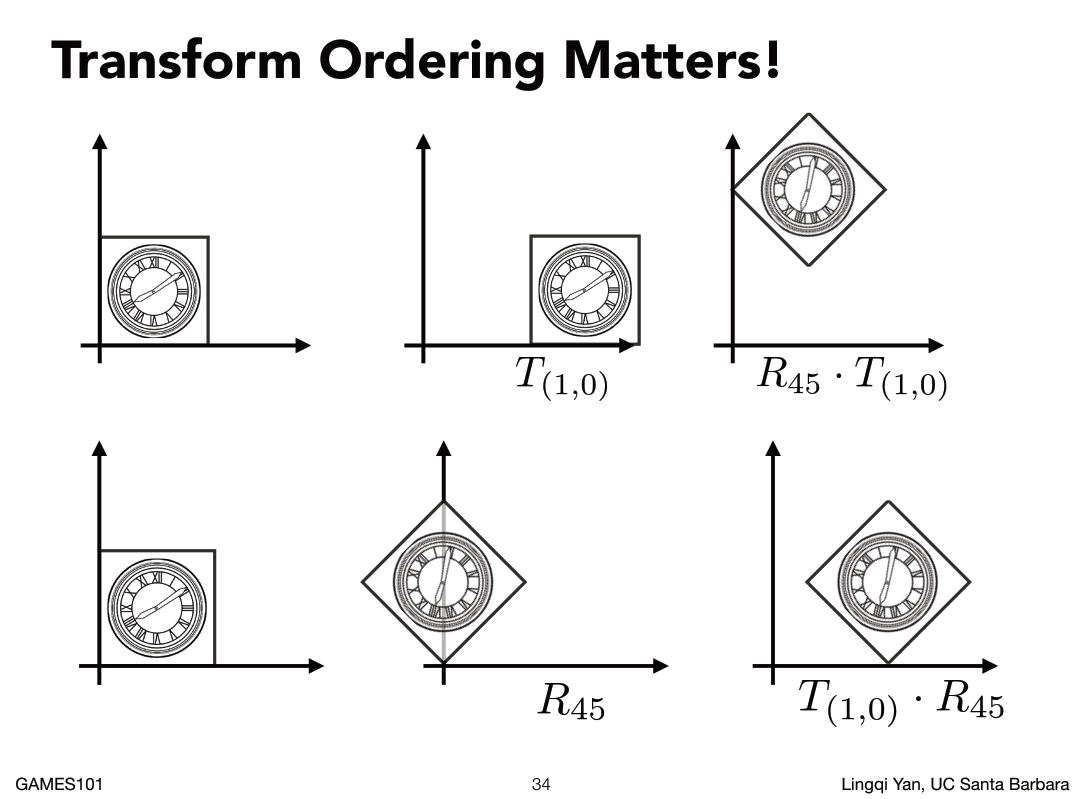
 先乘旋转矩阵再乘平移矩阵,也就是等号左边逐个变换逐个向左写,等会右边乘的时候也是从右往左乘(跟整数乘法正好相反),推广概念如下图:
先乘旋转矩阵再乘平移矩阵,也就是等号左边逐个变换逐个向左写,等会右边乘的时候也是从右往左乘(跟整数乘法正好相反),推广概念如下图:
 Tips:矩阵没有交换律,但是有结合律。可以把A1到An乘完得到一个矩阵在和向量相乘,也就是说,**一个矩阵就可以表示非常复杂的变换**
Tips:矩阵没有交换律,但是有结合律。可以把A1到An乘完得到一个矩阵在和向量相乘,也就是说,**一个矩阵就可以表示非常复杂的变换**
同样道理,变换既然可以合成也就可以分解。如下图: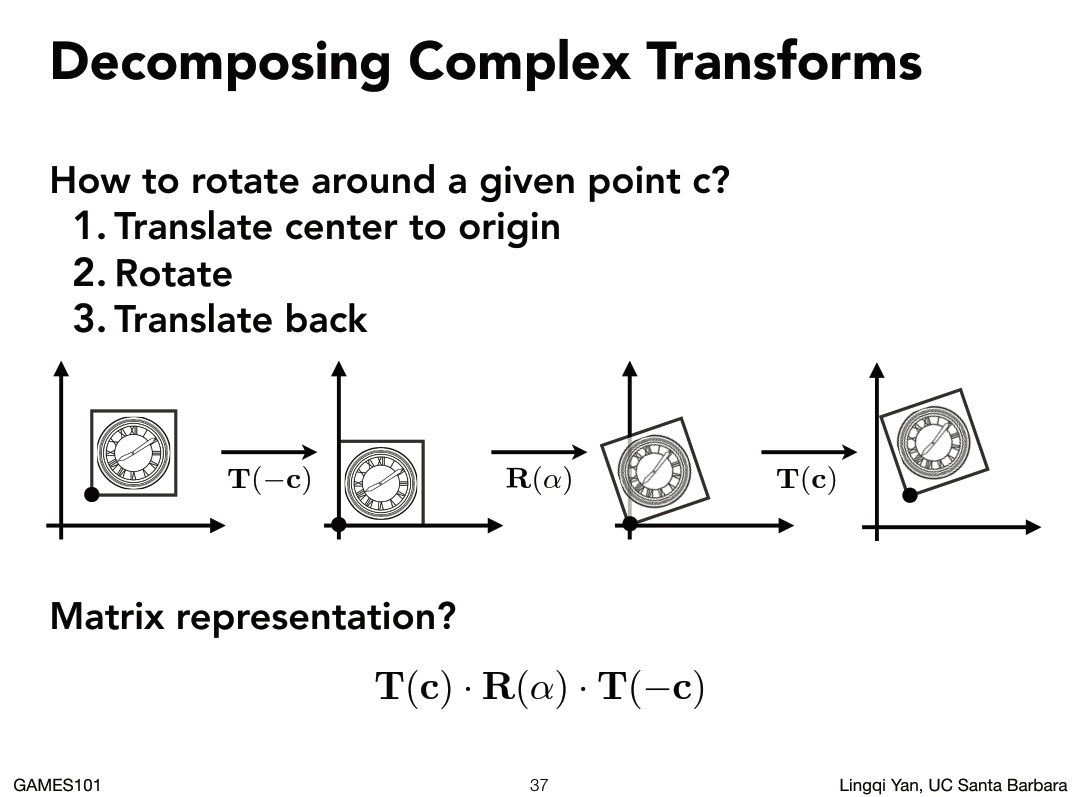
如果我们想已给定点为中心进行旋转,可以分解如图,先把这个点移到(0,0)点{移动一个-C},然后旋转,再移动回去{移动一个C}
三维变换
三维的变换就是把二维的变换拿过去做类比就可以(包括齐次坐标表示)。
三维空间也会有线性变换,三维空间也会有平移。也不希望三维空间的平移变成特殊现学,也就再次用齐次坐标,再加一个数。四维数表示三维空间的点和向量。
4X4矩阵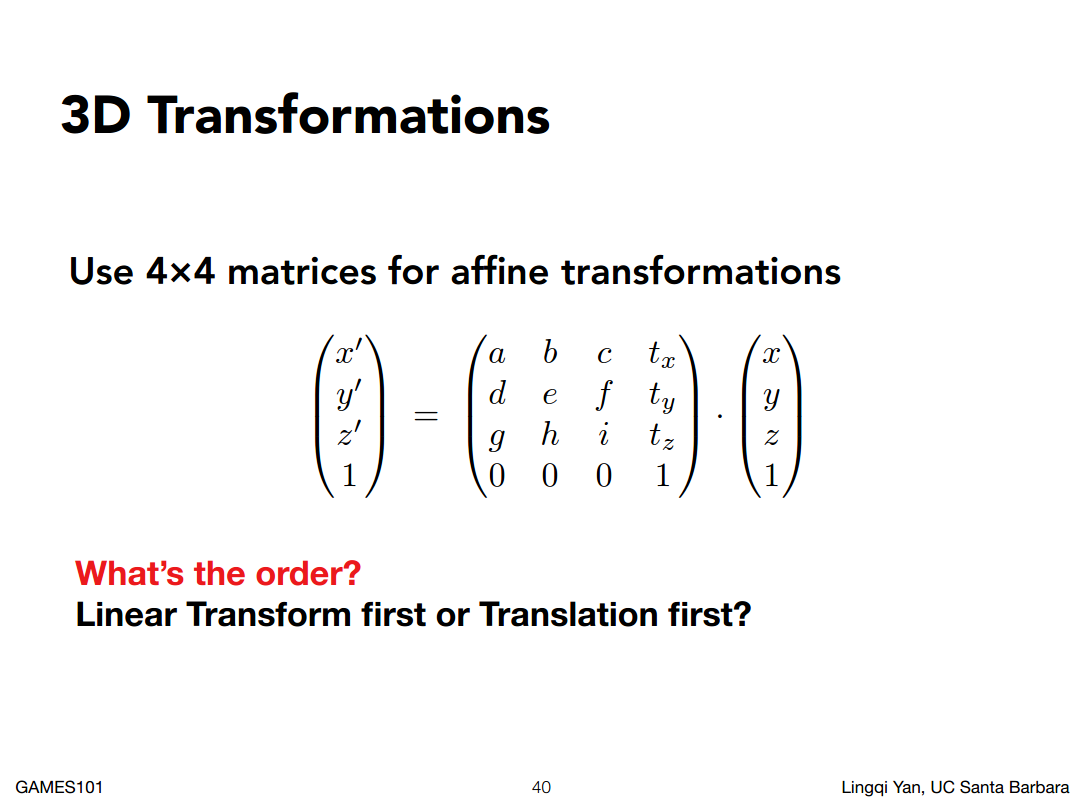
三维空间中 仿射变换的情况下, 最后一行肯定是(0,0,0,1)
问题
如上图的变换,是先表示的线性变换还是先表示的位移?
是先进行的线性变换,再进行的位移。遇到此类问题可以考虑不用齐次坐标的表示。
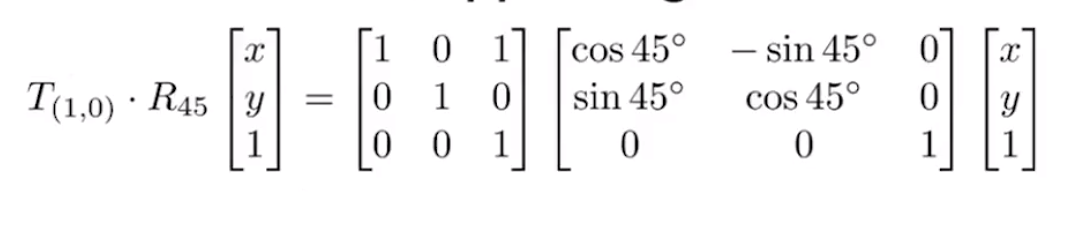
第四节 变换续
上节的补充
二维情况下,如果不考虑齐次坐标,变换可以用2x2的矩阵来表示,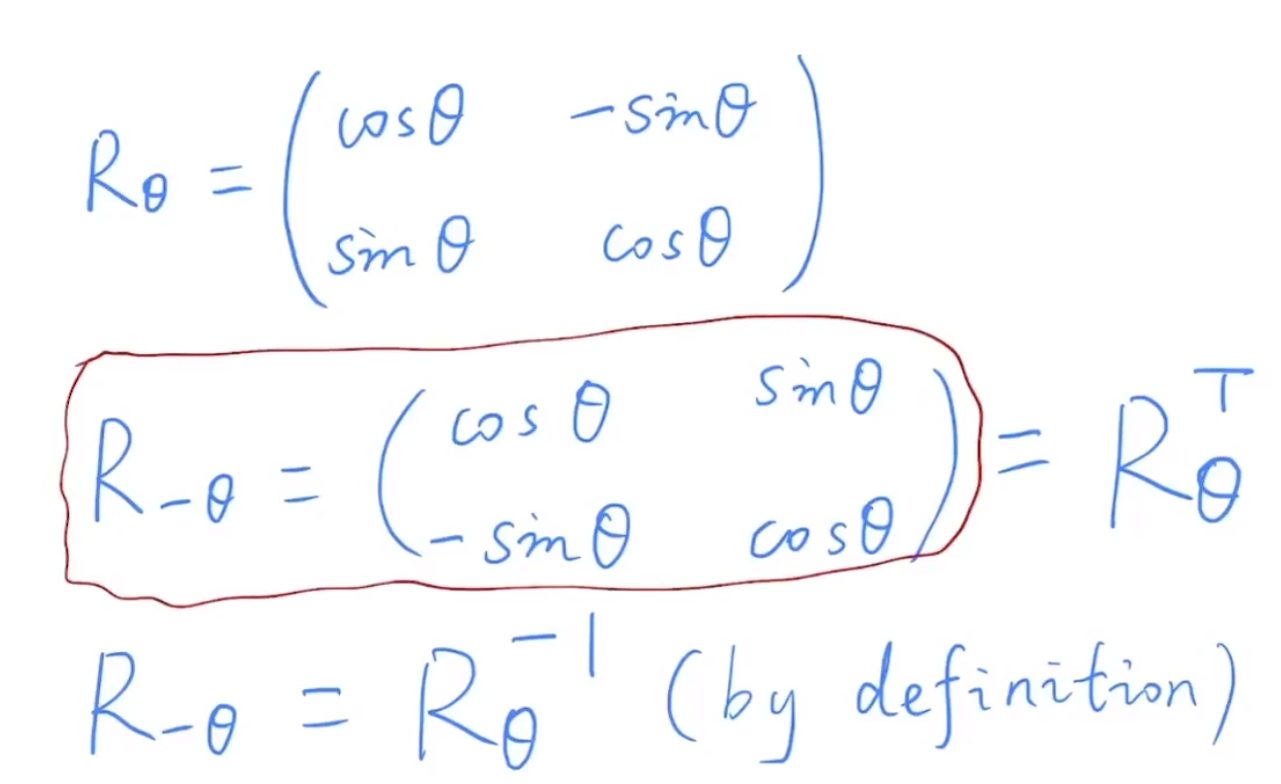
注意这里:
cos -θ 等于cosθ
sin -θ 等于-sinθ
这里有两个情况:
- 和上面的矩阵相比这样我们就发现,旋转θ角和旋转-θ角就是把这个矩阵做了一个转置(行列对换)。
- 从定义上来看,旋转θ角和旋转-θ角,应该是一个互逆的关系,旋转-θ角应该就是旋转θ角的到的矩阵的逆。
由此可以得出,如下图: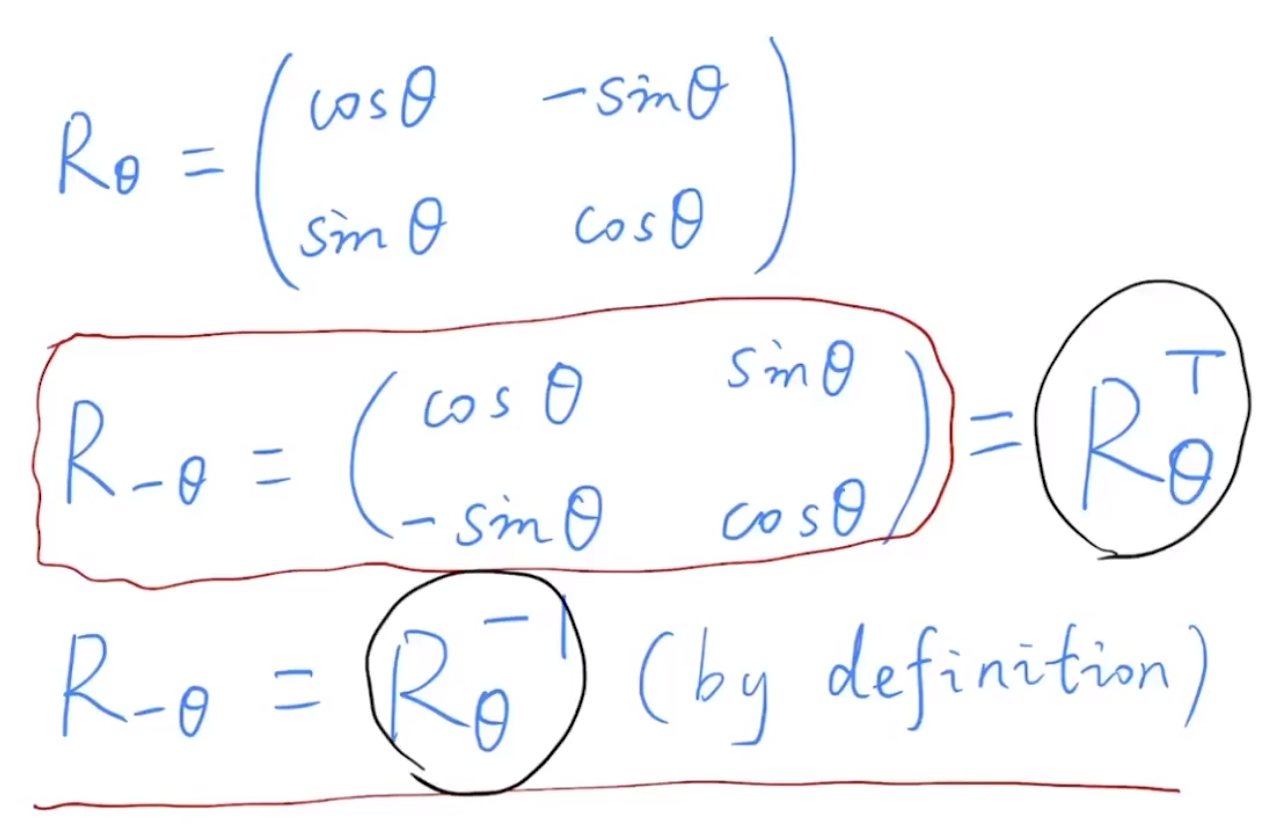 旋转矩阵的转置等于旋转矩阵的逆
tips:
在数学上如果一个矩阵的逆等于这个矩阵的转置,那么这个矩阵叫做正交矩阵。
##### 上节的复习
旋转矩阵的转置等于旋转矩阵的逆
tips:
在数学上如果一个矩阵的逆等于这个矩阵的转置,那么这个矩阵叫做正交矩阵。
##### 上节的复习
 ##### 本节
##### 本节
 把三维变换结束掉之后,重点是viewing变换。
##### 三维变换
把三维变换结束掉之后,重点是viewing变换。
##### 三维变换

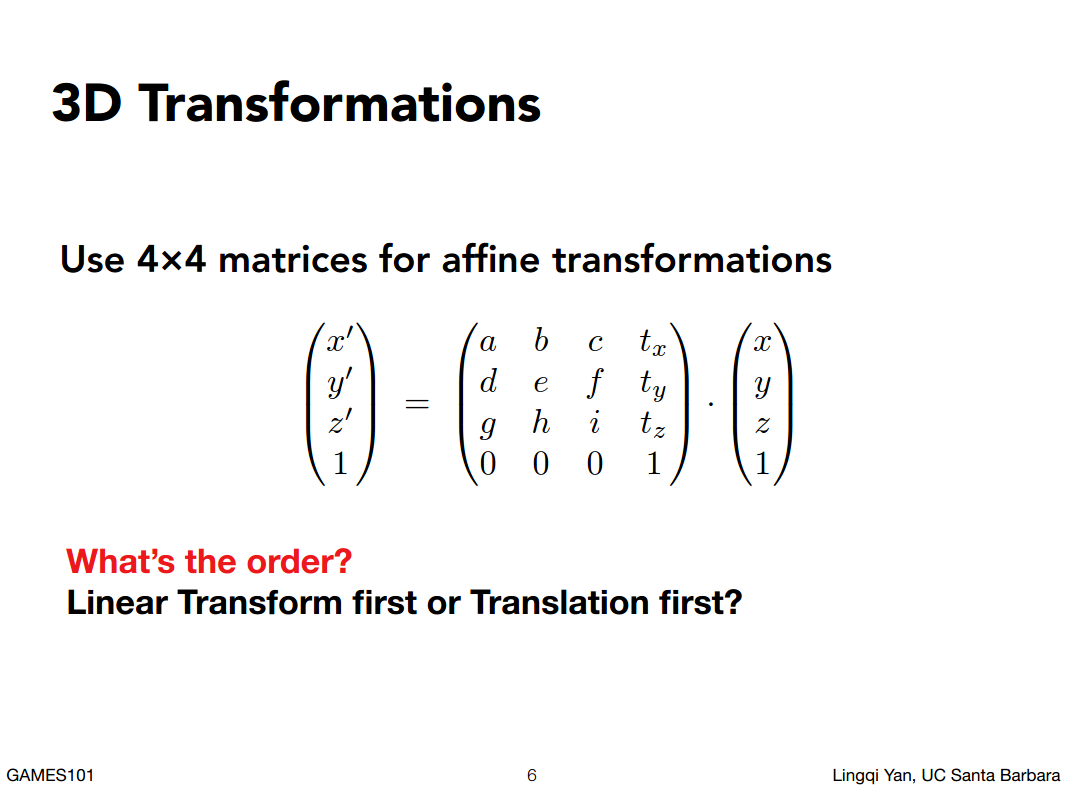

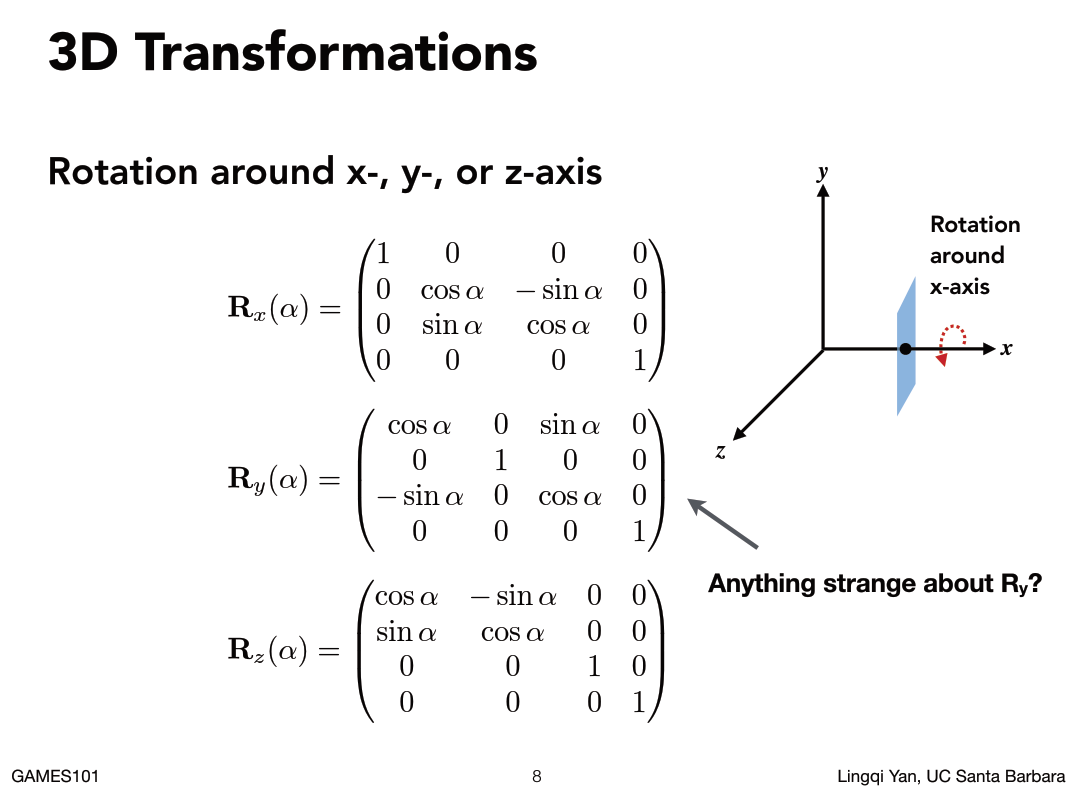 对于三维空间的旋转变换,如果直接考虑绕任意一个轴旋转是很复杂的,但是如果绕XYZ的话就会相对简单,比如绕X轴移动的平面,其X坐标是不会发生任何改变的,发生改变的是Y,Z两个轴的数值。所以Rx和Rz都是有一个轴是不发生任何改变。
对于三维空间的旋转变换,如果直接考虑绕任意一个轴旋转是很复杂的,但是如果绕XYZ的话就会相对简单,比如绕X轴移动的平面,其X坐标是不会发生任何改变的,发生改变的是Y,Z两个轴的数值。所以Rx和Rz都是有一个轴是不发生任何改变。
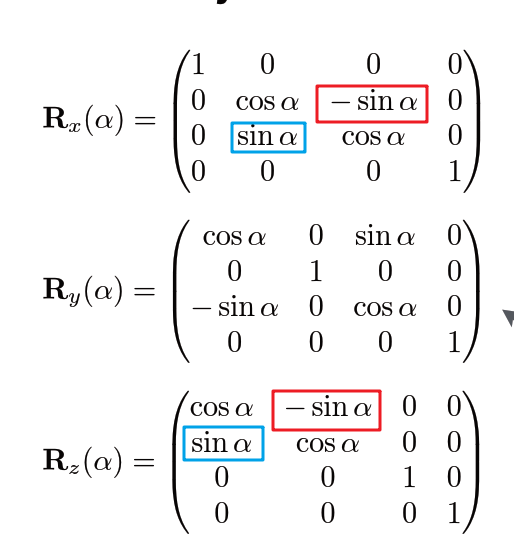
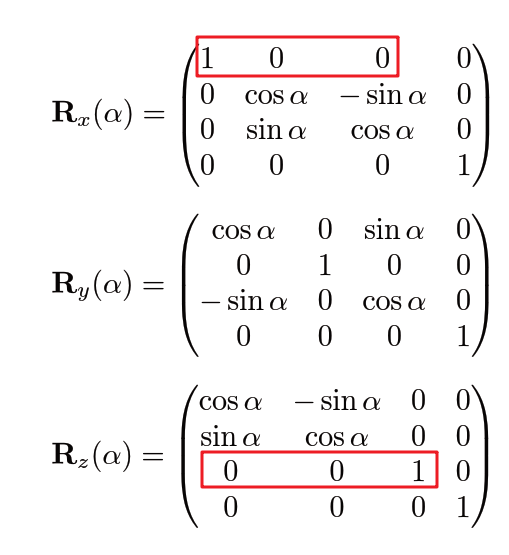 注意RxRz的符号是一致的,但是Ry是反的为什么呢,图上如果要的到Y就是Z叉乘X(xyzxyz循环对称性质),因为是反着的,所以结果符号是反的。
> 这是因为二维平面定义时,逆时针实际是在三维从Z正向看,因此三维绕Y旋转,逆时针实际上是从Z向X运动,但是旋转矩阵的行列对应关系是X向Z转,取逆(转置)就得到了。
注意RxRz的符号是一致的,但是Ry是反的为什么呢,图上如果要的到Y就是Z叉乘X(xyzxyz循环对称性质),因为是反着的,所以结果符号是反的。
> 这是因为二维平面定义时,逆时针实际是在三维从Z正向看,因此三维绕Y旋转,逆时针实际上是从Z向X运动,但是旋转矩阵的行列对应关系是X向Z转,取逆(转置)就得到了。
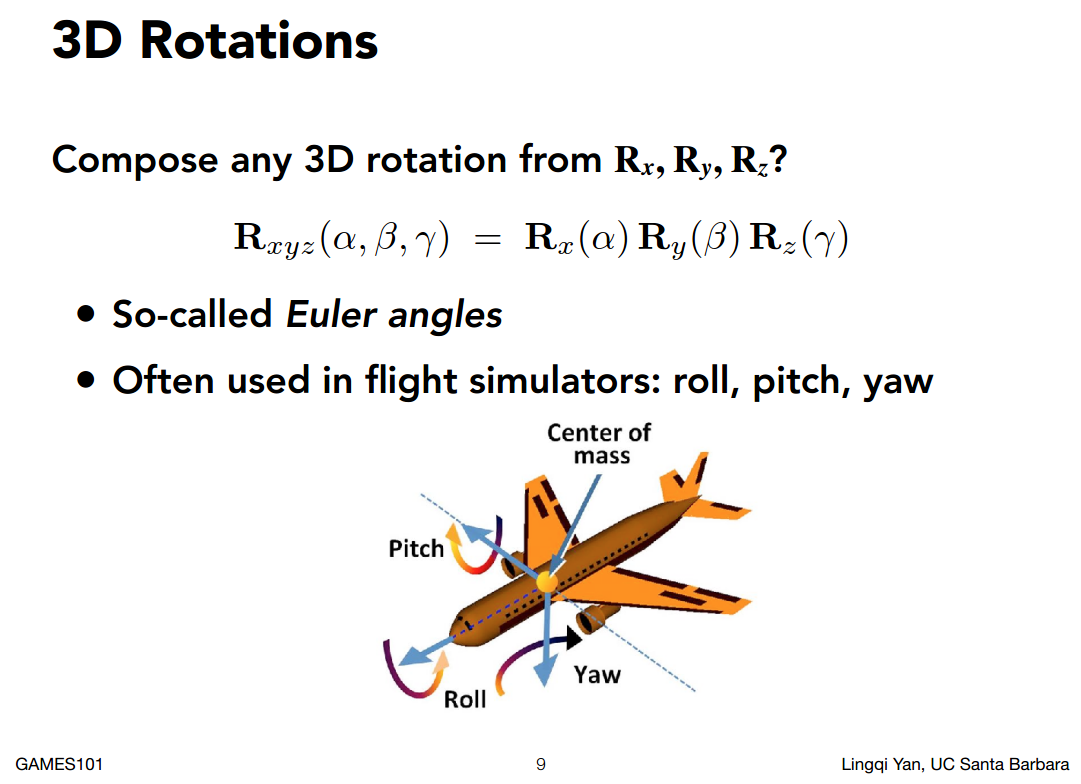
 对于任意一个旋转,我们可以把它分解为绕X绕Y绕Z旋转。
对于任意一个旋转,我们可以把它分解为绕X绕Y绕Z旋转。
 默认向量n的起点在原点,如果不是的话,可以用上一节的方法,先把它移动到原点,变换完再挪回去。
##### Viewing变换
最终目的,是把三维空间里面的东西变成二维的。
默认向量n的起点在原点,如果不是的话,可以用上一节的方法,先把它移动到原点,变换完再挪回去。
##### Viewing变换
最终目的,是把三维空间里面的东西变成二维的。
 |现实生活里拍照片动作|viewing变换动作|
|------------------|--------------|
|找好位置摆好pos|模型变换 model transformation|
|找到一个好的角度|视图变换 view transformation|
|茄子|投影变换 projection transformation|
简称MVP变换
怎么做view变换呢?
|现实生活里拍照片动作|viewing变换动作|
|------------------|--------------|
|找好位置摆好pos|模型变换 model transformation|
|找到一个好的角度|视图变换 view transformation|
|茄子|投影变换 projection transformation|
简称MVP变换
怎么做view变换呢?
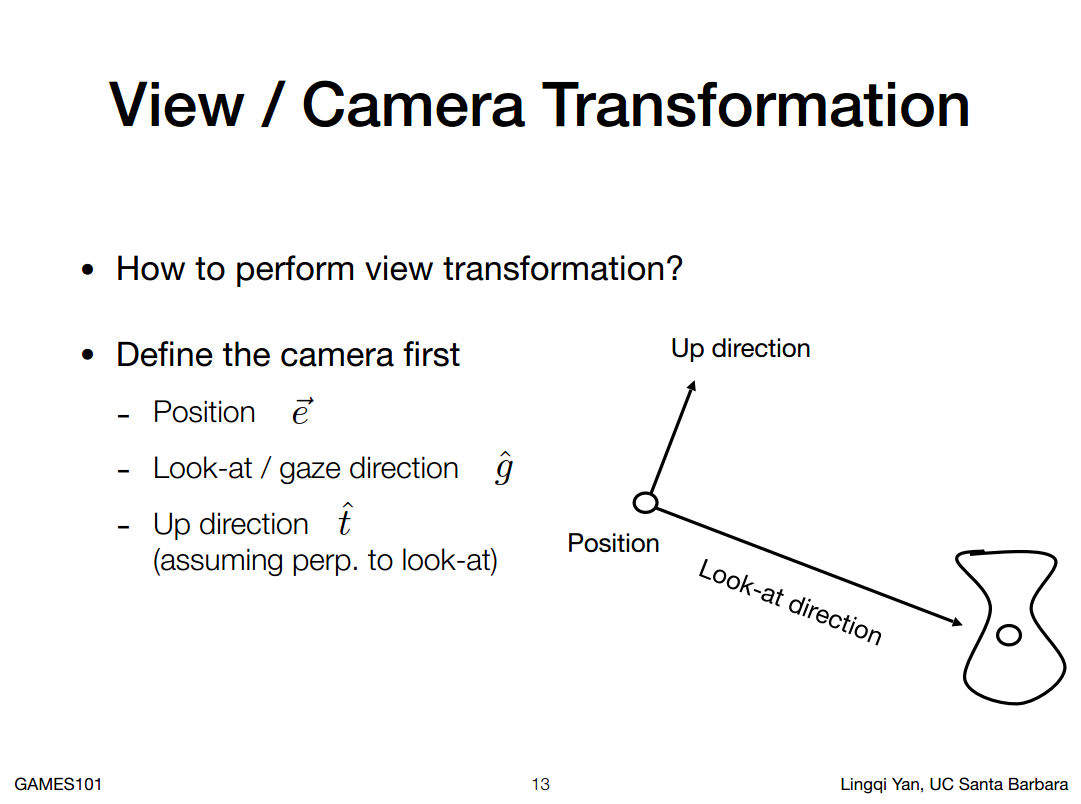
- 位置 往哪看
- 往哪看
- 相机本身的向上方向
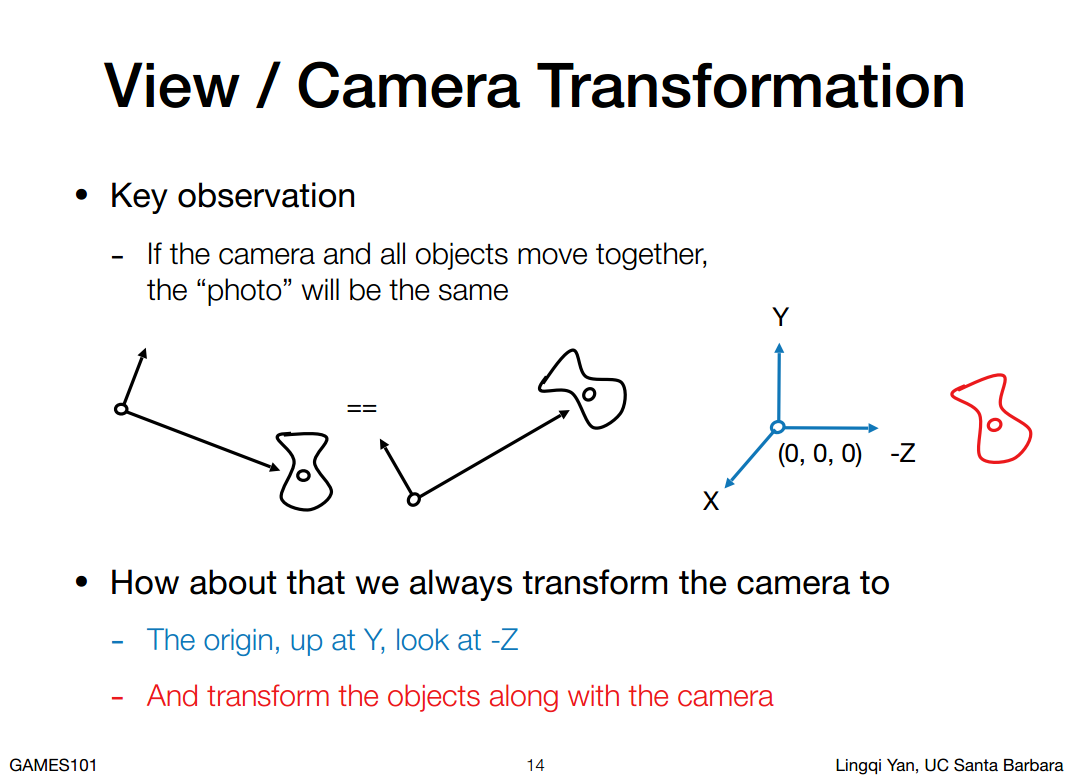
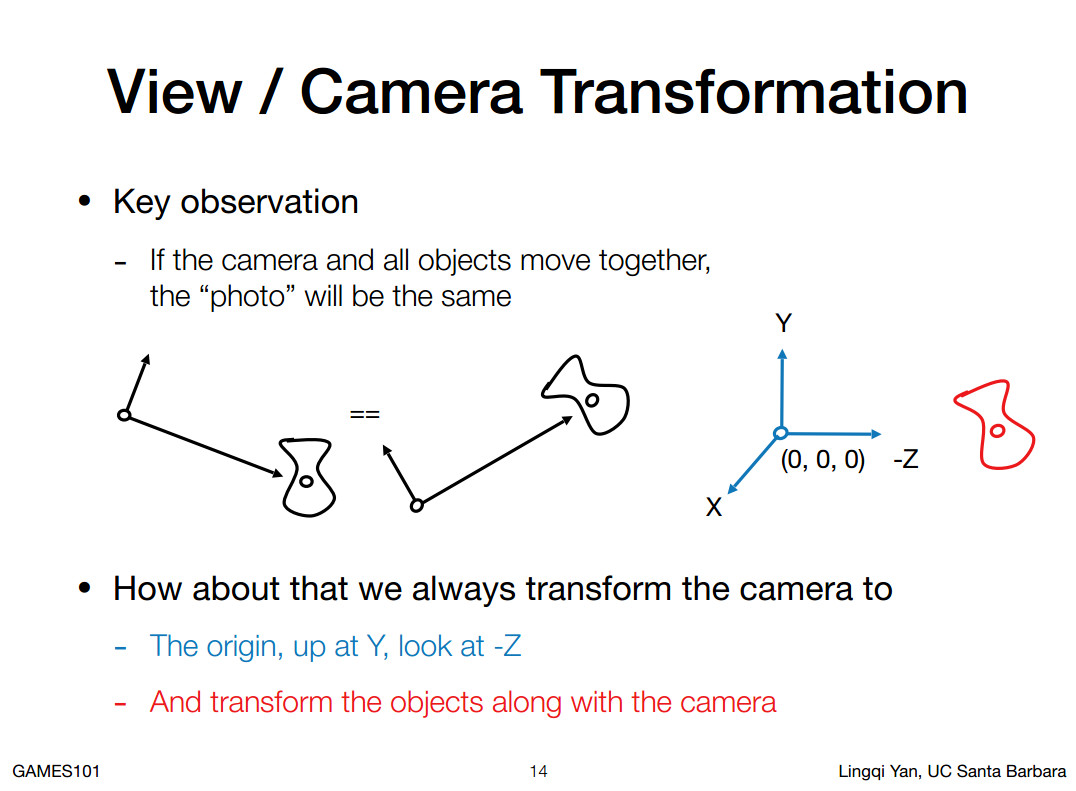
注意这里还是右手坐标系,可以使用右手螺旋定则判定。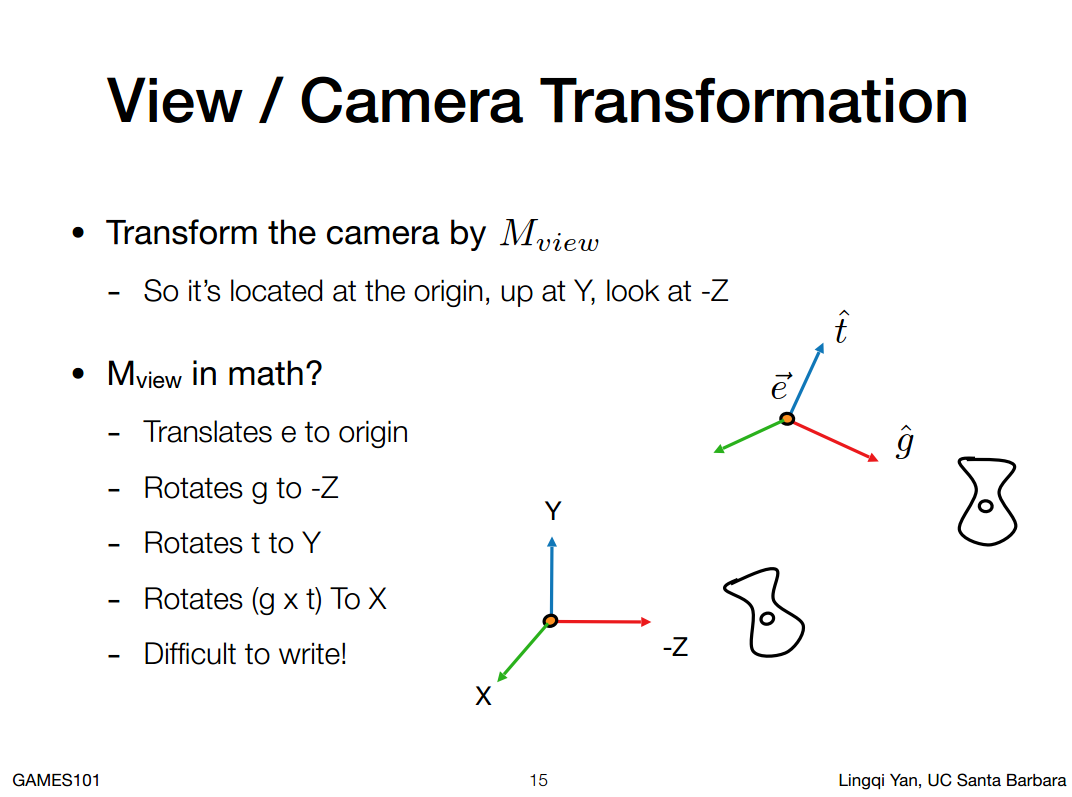
怎么把这种变换表示成矩阵呢?
- 位移: 注意应该先做线性变换在做平移,但是为了理解方便这里先做了平移,后做线性变换,但是接下来往左写,是一样的。
- 旋转:这里把某个向量旋转成标准轴不好实现,但是反过来把某个标准轴旋转成某个向量好实现,所以我们就等于先求出逆变换,(这里的矩阵逆用的很巧妙),怎么对一个旋转矩阵求逆呢?利用旋转矩阵是正交矩阵,正交矩阵的逆就是它的转置(本节课开始证明的)。
- 这个Mview矩阵就可以把摄影机移动到零点,同理也可以把其他所有东西移动到相对位置上。视图变换
 总结:
1. 任何时候只要相机和物体应用同样的变换或者位移,结果不变。
2. 视图变换操作的是相机,其他物体跟着变换。
##### Projection transforamtion投影变换
1. Orthographic projection 正交投影
2. Perspective projection 透视投影
总结:
1. 任何时候只要相机和物体应用同样的变换或者位移,结果不变。
2. 视图变换操作的是相机,其他物体跟着变换。
##### Projection transforamtion投影变换
1. Orthographic projection 正交投影
2. Perspective projection 透视投影
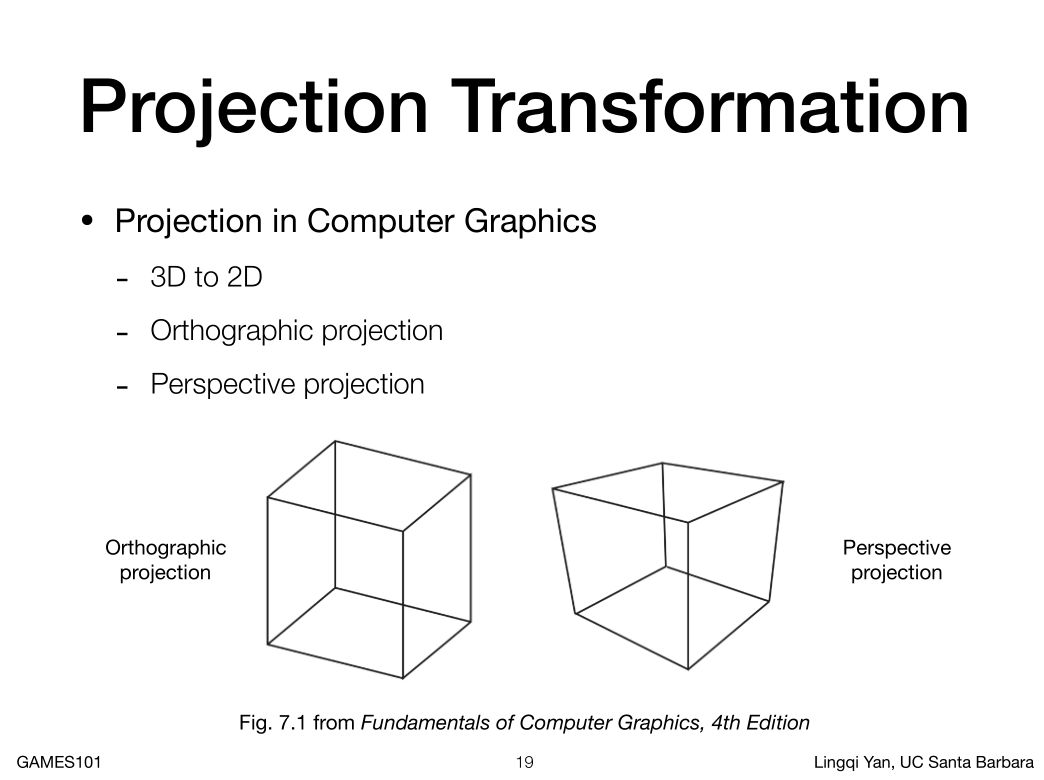 左边的正交投影,平行线永远平行(多用于工程制图)
右边透视投影近大远小,平行线延长终会相交(人眼)
左边的正交投影,平行线永远平行(多用于工程制图)
右边透视投影近大远小,平行线延长终会相交(人眼)
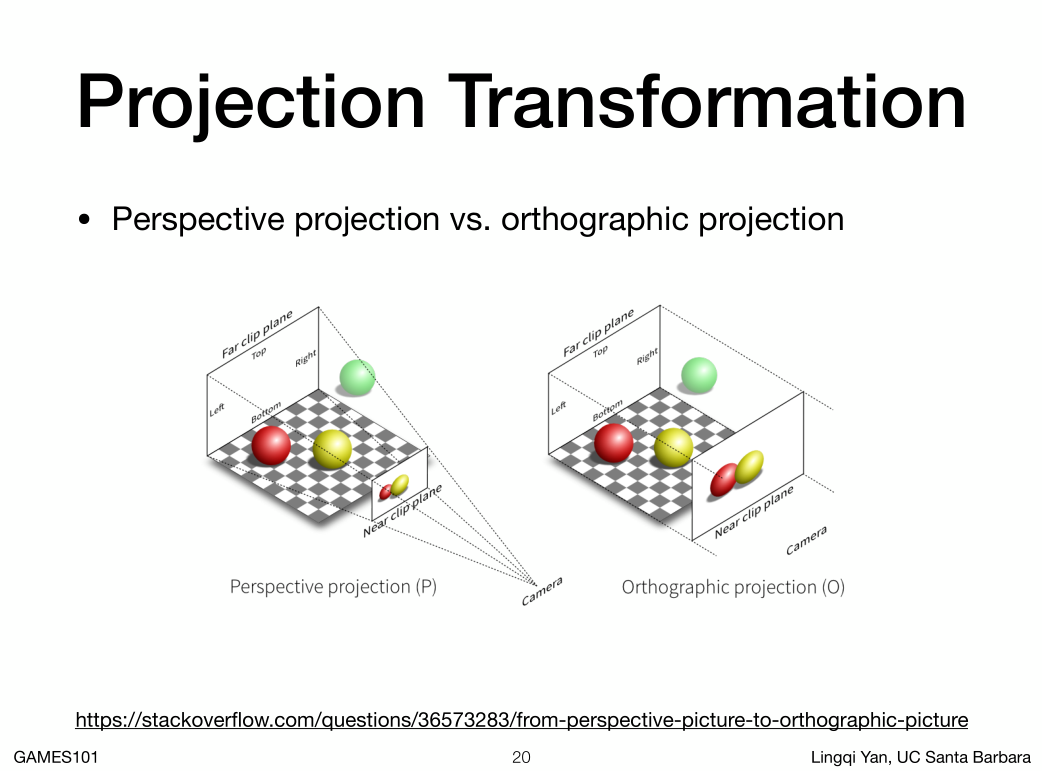 左边透视投影,我们认为某个位置上的摄影机是一个点,去连出空间中的一个四棱锥。
右边正交投影,假设摄影机离得无限远,直到近和远的平面一样大。
##### 正交投影
正交投影相对好理解。
左边透视投影,我们认为某个位置上的摄影机是一个点,去连出空间中的一个四棱锥。
右边正交投影,假设摄影机离得无限远,直到近和远的平面一样大。
##### 正交投影
正交投影相对好理解。
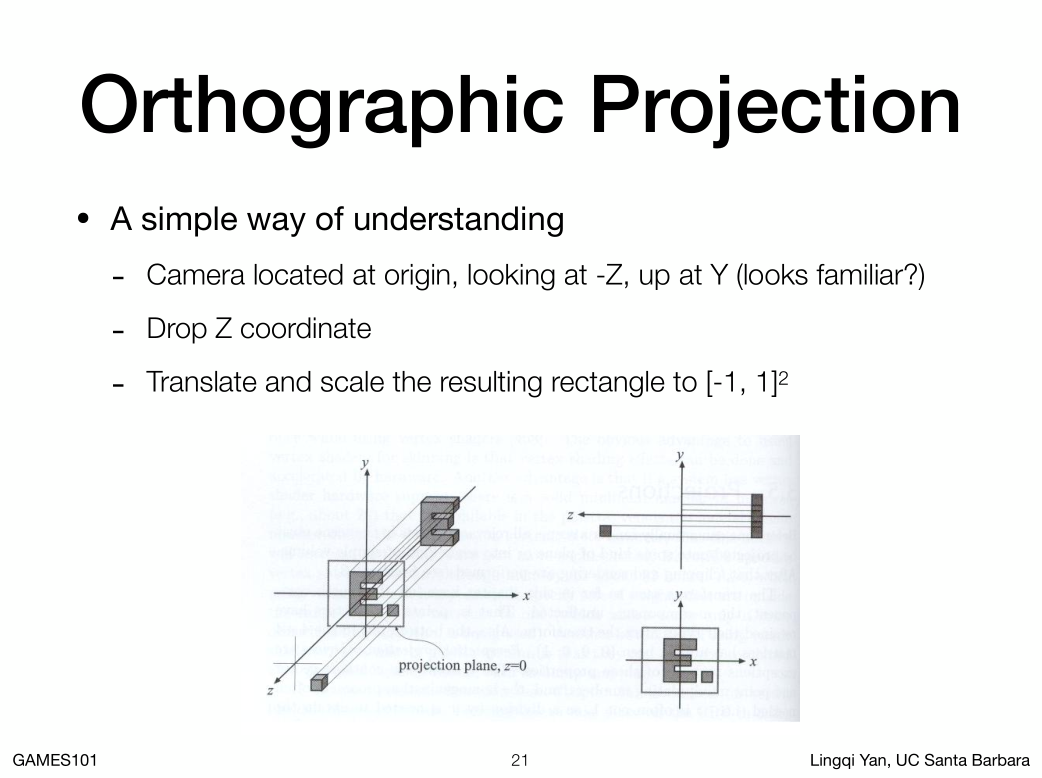 理解:
1. 定义摄影机在原点,看向-Z,顶部朝Y
2. 把Z轴坐标丢掉
3. 把结果都挪到-1,1
实际操作:
理解:
1. 定义摄影机在原点,看向-Z,顶部朝Y
2. 把Z轴坐标丢掉
3. 把结果都挪到-1,1
实际操作:
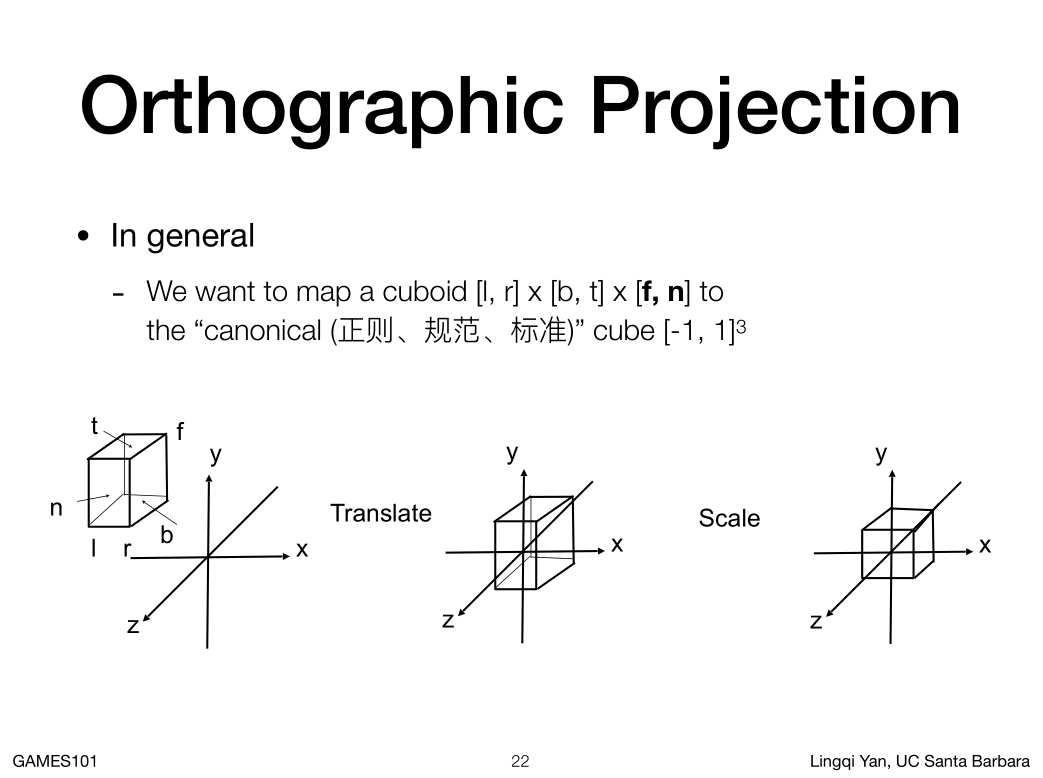 1. 首先定义空间中的一个立方体,
2. 在xyz三轴找到对应的坐标 left,right,bottom,top,far,near,有了这六个数就可以定义这个立方体
3. 映射到canonical cube -1,1,
1. 首先定义空间中的一个立方体,
2. 在xyz三轴找到对应的坐标 left,right,bottom,top,far,near,有了这六个数就可以定义这个立方体
3. 映射到canonical cube -1,1,
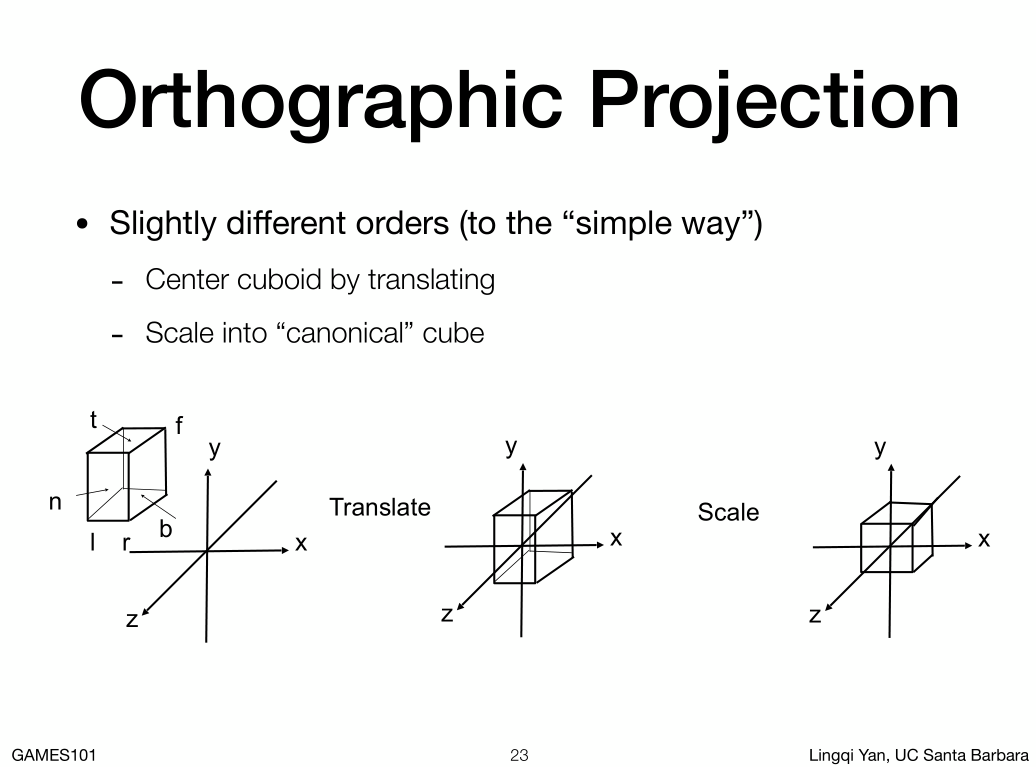
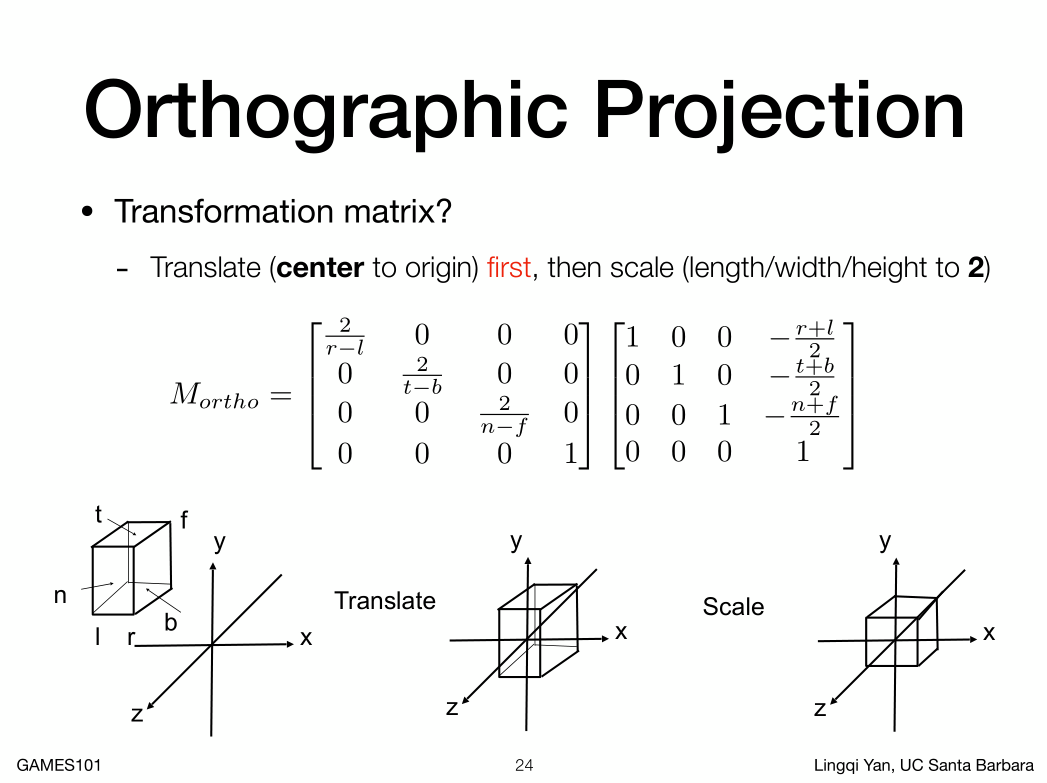
把这个变换写成矩阵的形式:
- 注意这里是先做平移,后面在做缩放
- 平移X值是指先求出矩形的长r+l除以2得到长的中心,在移动负中心的位置就是移动到x轴的中心,其它轴以此类推。
- 缩放X值,是先求出x的覆盖范围也就是长度r-l,跟比2的倍数也就是2/r-l,为什么是2,因为canonical的x长度是-1到1长度2。有了这个倍数,在对其进行缩放就把元素匹配到canonical cube里了。其它轴以此类推。
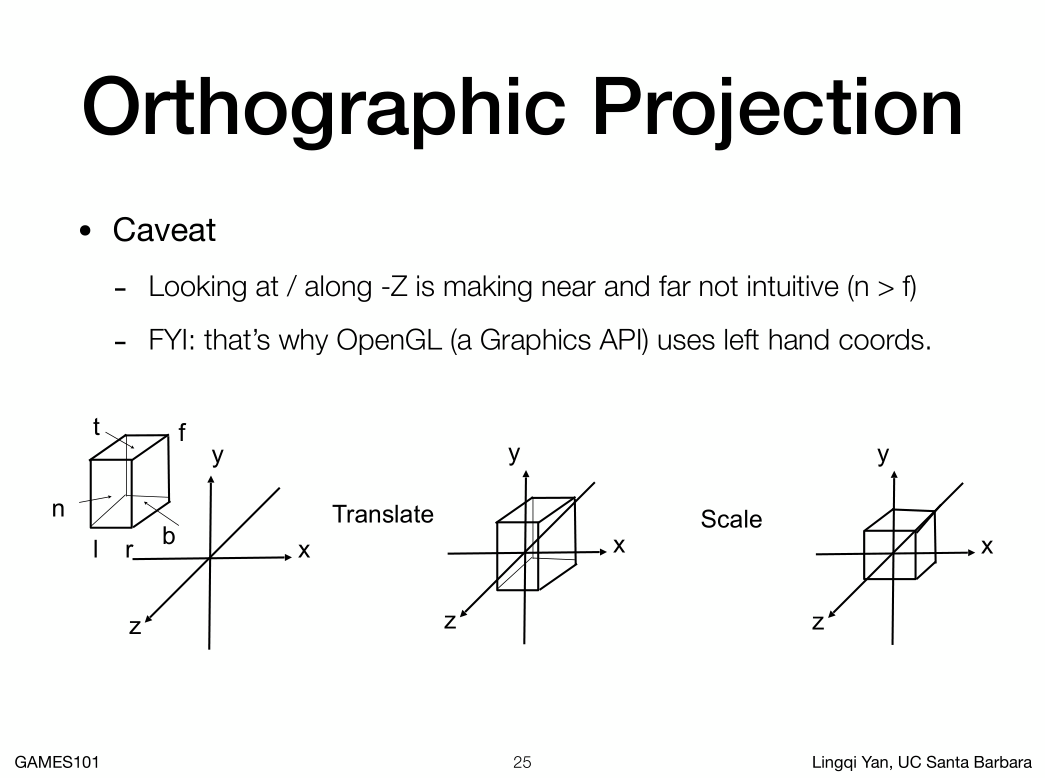 1. 因为摄影机看向-Z,所以这里的far是小于near的(-10小于-1)**
2. 这里opengl 左手系就是far大于near,但是左手系会带来别的问题,x叉乘Y不等于Z等。
##### 透视投影
1. 因为摄影机看向-Z,所以这里的far是小于near的(-10小于-1)**
2. 这里opengl 左手系就是far大于near,但是左手系会带来别的问题,x叉乘Y不等于Z等。
##### 透视投影
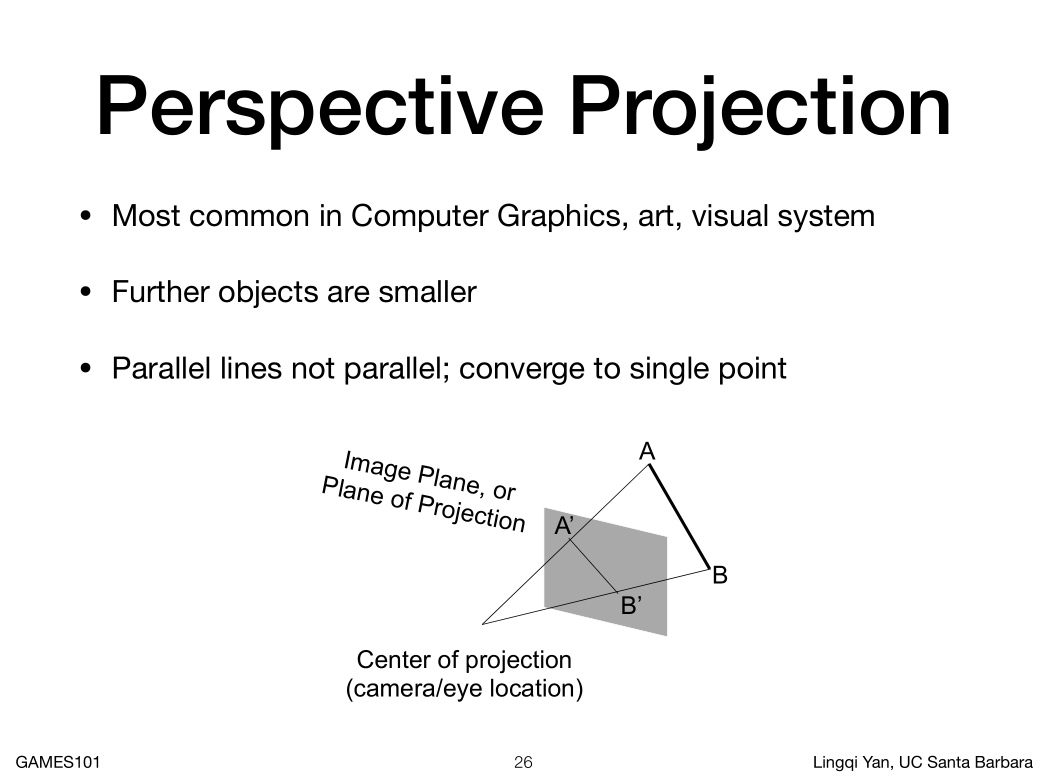 1. 用的最广泛的投影
2. 进大远小
3. 平行线不平行,相交与一点
1. 用的最广泛的投影
2. 进大远小
3. 平行线不平行,相交与一点

 在继续学习之前
这里复习了一下齐次坐标,当一个点(xyz1)的每个数都乘以任意一个数,表示的点不变。
例如(1,0,0,1)和(2,0,0,2)都代表(1,0,0)
简单,但是有用。
在继续学习之前
这里复习了一下齐次坐标,当一个点(xyz1)的每个数都乘以任意一个数,表示的点不变。
例如(1,0,0,1)和(2,0,0,2)都代表(1,0,0)
简单,但是有用。
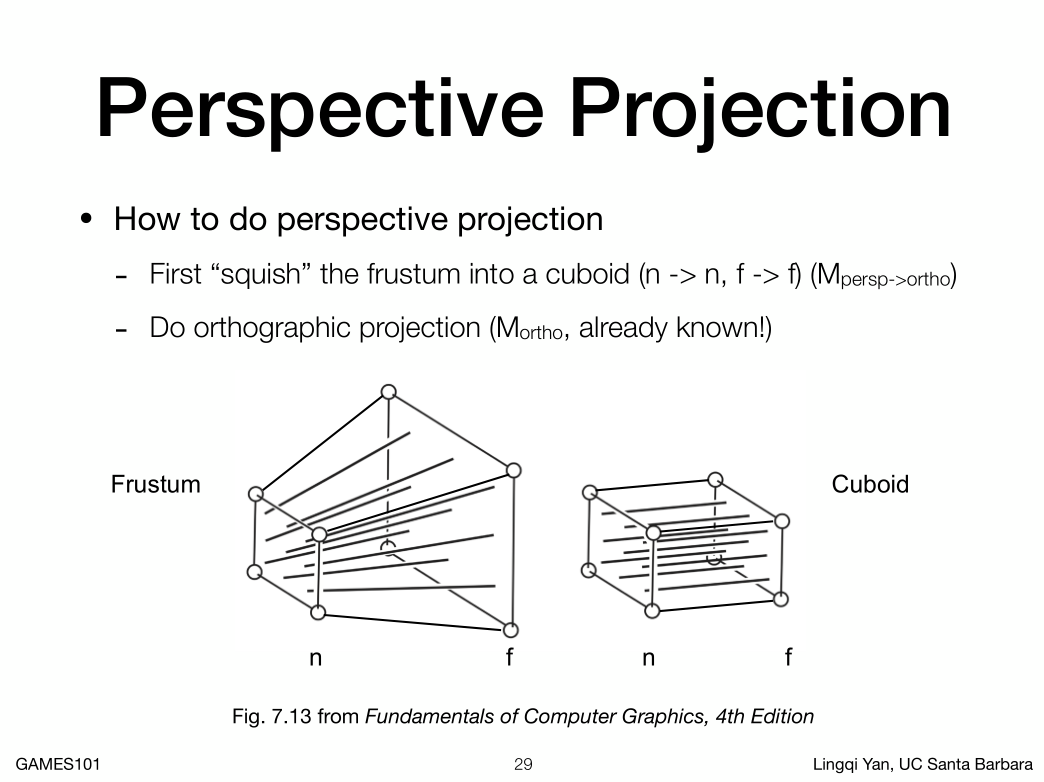 先定义个Frustum(平截头体),跟右边的Cuboid(长方体)对比,我们会发现只有远端的平面不一样,假如我们把远端的平面缩放到跟近端的平面一样,那就是跟正交投影一样了。
也就是我们把投射投影拆成了两步:
1. 把远端的平面挤压到跟近端的平面一样,也就是把frustum变成cuboid。也就是求一个矩阵MPersp->Ortho
2. 做一下正交投影
先定义个Frustum(平截头体),跟右边的Cuboid(长方体)对比,我们会发现只有远端的平面不一样,假如我们把远端的平面缩放到跟近端的平面一样,那就是跟正交投影一样了。
也就是我们把投射投影拆成了两步:
1. 把远端的平面挤压到跟近端的平面一样,也就是把frustum变成cuboid。也就是求一个矩阵MPersp->Ortho
2. 做一下正交投影
规定:
- 近平面任何一点都不变。
- 远处的平面 Z值是f,操作完之后 远处的平面Z值仍然是F,同理,近平面的Z也不变。
- 远平面的中心点,缩放完之后还是中心点,坐标也是完全不变的。
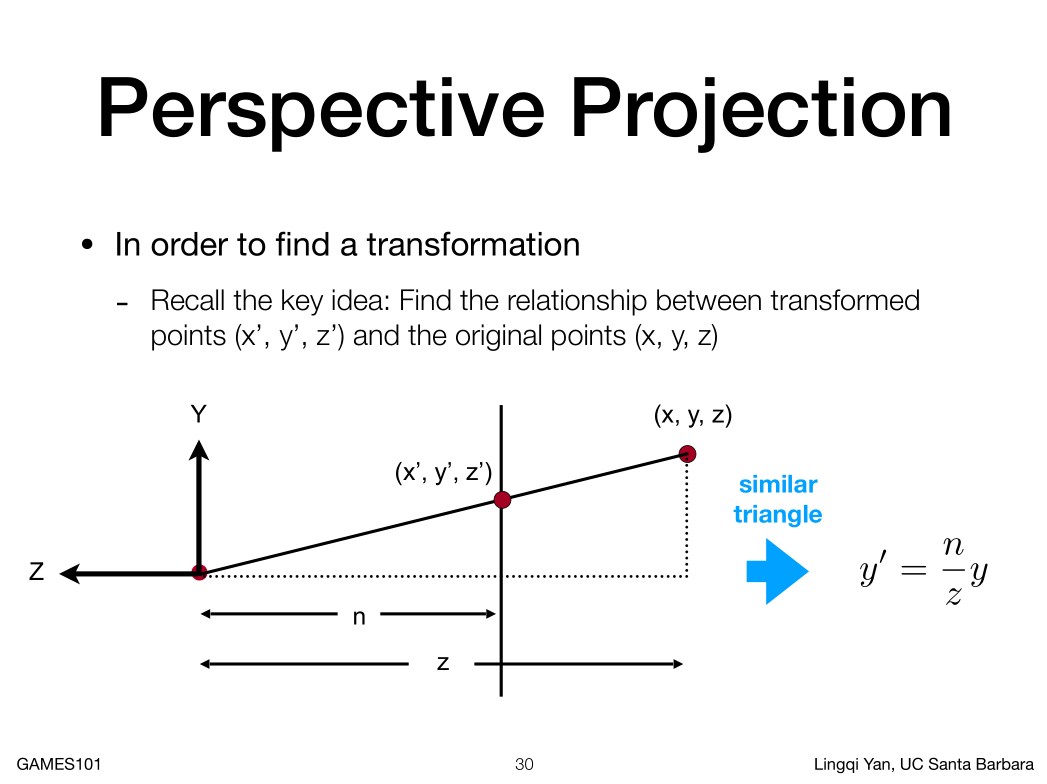 挤压这步怎么做,也就是怎么求一个矩阵MPersp?
假设我们从侧面望Frustum上看,这里最左边是摄影机,朝-Z看,如上图。
看到两个相似三角形,根据相似三角形定理,Y'比上Y等于N比上Z
所以我们可以得到 y' = (n/z)*y
挤压这步怎么做,也就是怎么求一个矩阵MPersp?
假设我们从侧面望Frustum上看,这里最左边是摄影机,朝-Z看,如上图。
看到两个相似三角形,根据相似三角形定理,Y'比上Y等于N比上Z
所以我们可以得到 y' = (n/z)*y
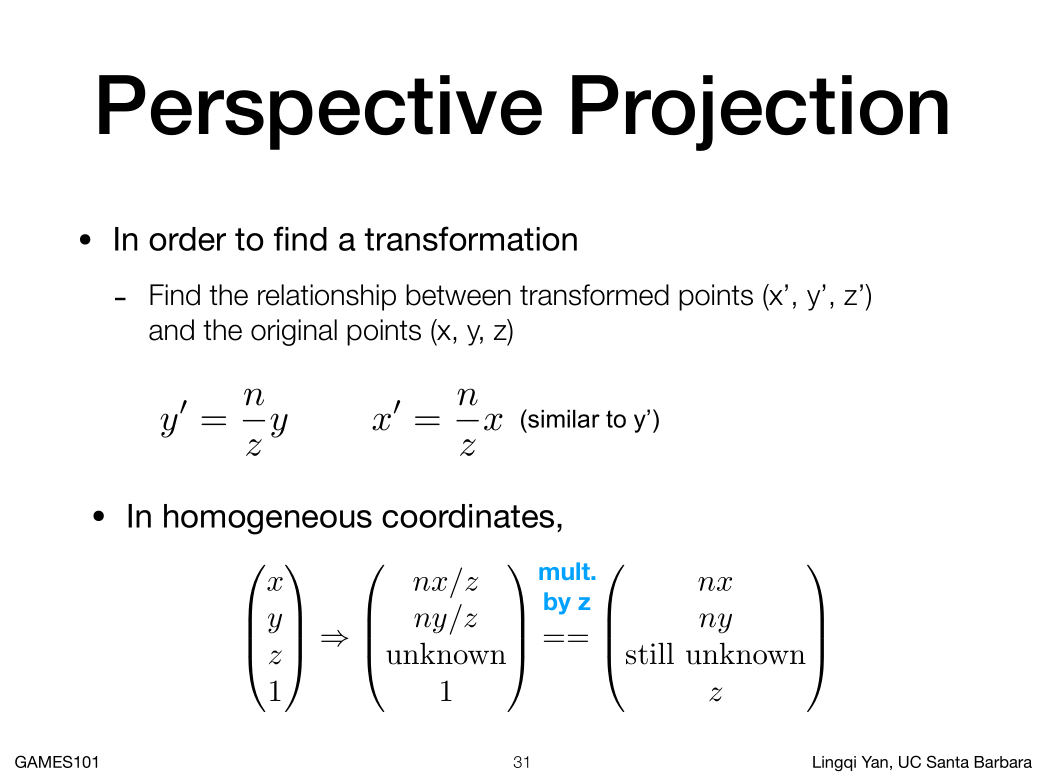 同理我们可以得到 X' = (n/z)*x
现在我们知道XY在变换之后的结果,我们可以利用齐次坐标的属性共同乘以Z。
同理我们可以得到 X' = (n/z)*x
现在我们知道XY在变换之后的结果,我们可以利用齐次坐标的属性共同乘以Z。
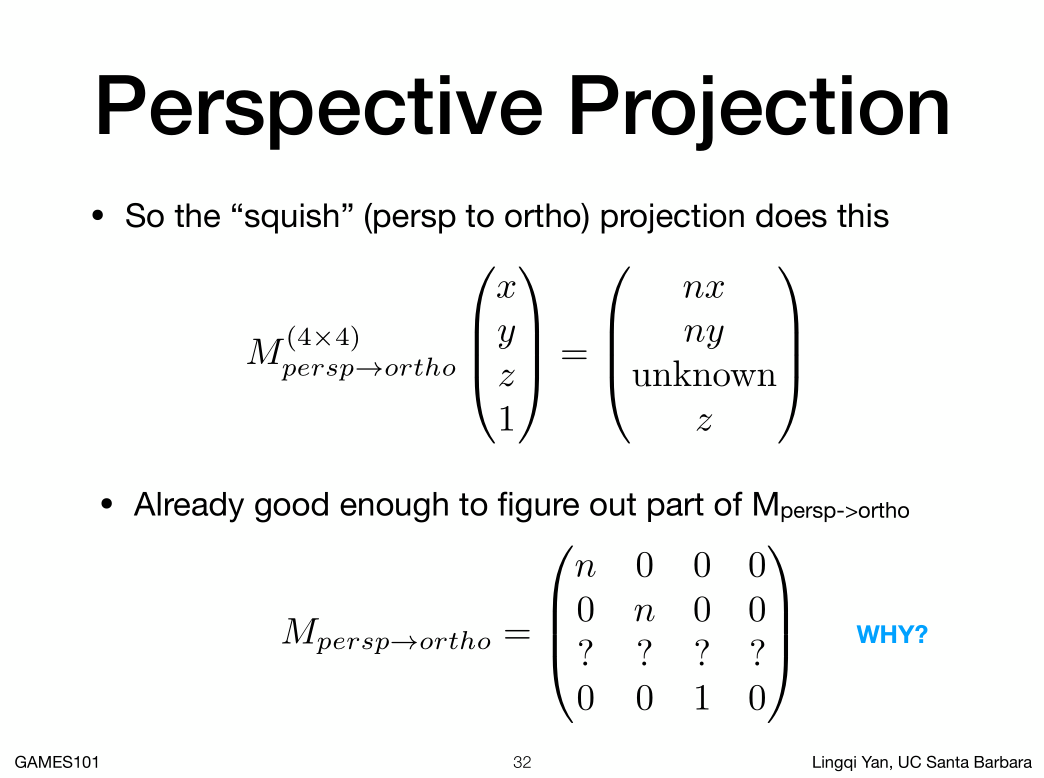 跟我们知道的结果,我们可以反推出矩阵:
如上图上方4*4矩阵乘以向量(x,y,z,1),得到(nx,ny,unknow,z)。
我们知道矩阵乘法是,一行乘一列,X是第一行第一列,也就是4*4矩阵的第一行点乘向量(x,y,z,1)一列,
得到nx,所以矩阵的第一行就只能是 (n,0,0,0).
跟我们知道的结果,我们可以反推出矩阵:
如上图上方4*4矩阵乘以向量(x,y,z,1),得到(nx,ny,unknow,z)。
我们知道矩阵乘法是,一行乘一列,X是第一行第一列,也就是4*4矩阵的第一行点乘向量(x,y,z,1)一列,
得到nx,所以矩阵的第一行就只能是 (n,0,0,0).
 两个观察发现:
1. 任何点在近平面上是完全不变的。
2. 任何点的z坐标值在远平面也是完全不变的。远平面的中心点,缩放完之后还是中心点,坐标也是完全不变的
根据这两个发现:
两个观察发现:
1. 任何点在近平面上是完全不变的。
2. 任何点的z坐标值在远平面也是完全不变的。远平面的中心点,缩放完之后还是中心点,坐标也是完全不变的
根据这两个发现:
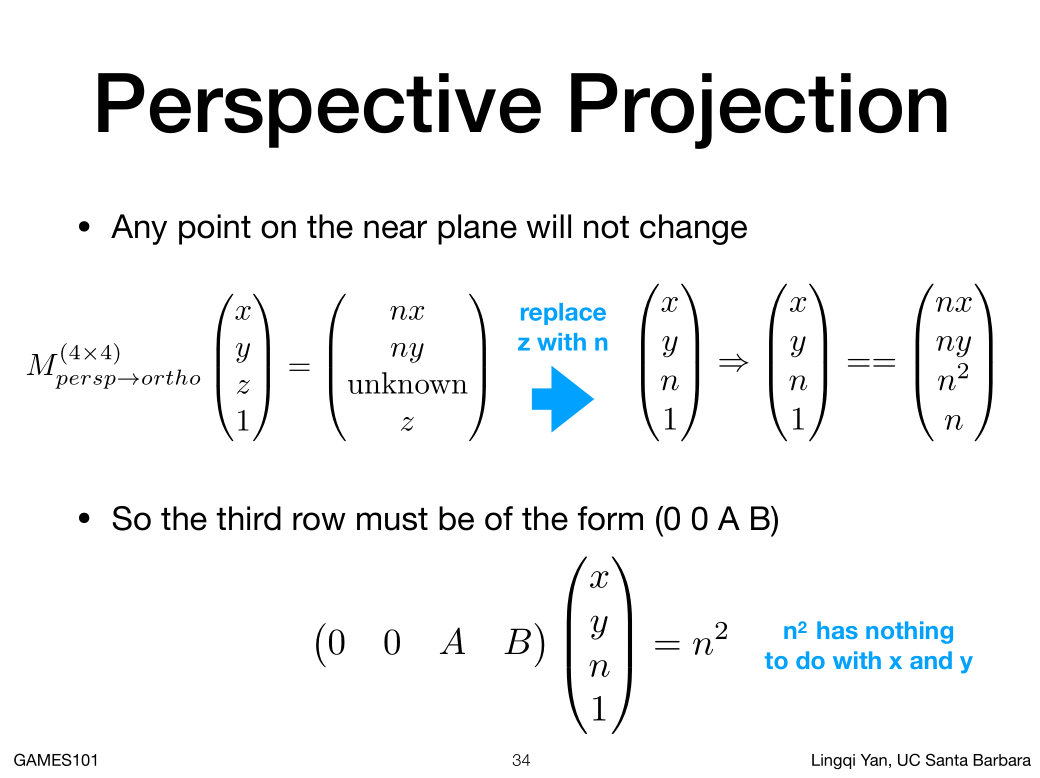 这里利用了齐次坐标的特性,把(x,y,n,1)四个数同时乘以n变成(nx,ny,n平方,n)
在利用任何点在近平面完全不变可以列出等式:
第三行的n平方 等于 矩阵M的第三行乘以向量第一列(x,y,n,1)
这里利用了齐次坐标的特性,把(x,y,n,1)四个数同时乘以n变成(nx,ny,n平方,n)
在利用任何点在近平面完全不变可以列出等式:
第三行的n平方 等于 矩阵M的第三行乘以向量第一列(x,y,n,1)
 远平面的中心点,缩放完之后还是中心点,坐标也是完全不变的,利用了齐次坐标的特性,把(0,0,f,1)四个数同时乘以f变成(0,0,f平方,f)
为啥必须乘以f,是因为我们希望最后以为是Z也就是远平面的z也就是f值:
远平面的中心点,缩放完之后还是中心点,坐标也是完全不变的,利用了齐次坐标的特性,把(0,0,f,1)四个数同时乘以f变成(0,0,f平方,f)
为啥必须乘以f,是因为我们希望最后以为是Z也就是远平面的z也就是f值:
 得到两个等式:
得到两个等式:
 根据这两个等式,我们可以解出A和B。
这里利用了完全平方公式。
根据这两个等式,我们可以解出A和B。
这里利用了完全平方公式。
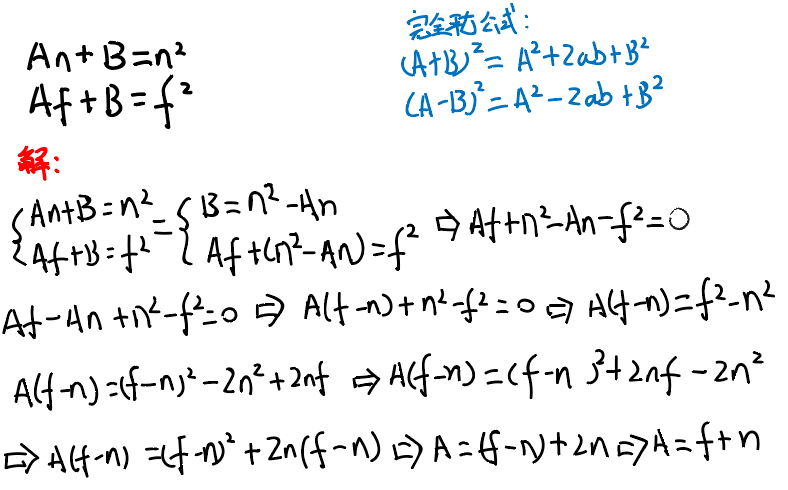 课后问题:
对于Frustum,我们知道变换完之后远平面和近平面的z是不变的,那中间任意一点的z呢?是会被推向近平面还是推向远平面?
变远。
很奇怪的是数值变的异常大,比如我指认n是-3 f是-5,得到矩阵之后,给定一个中间点(0,1,-4,1)(这里必须是点,也就是w是1,因为向量平移不变),结果是(0,-3,17,-4) ,由于齐次坐标(x/w,y/w,z/w,w/w),所以结果是(0,0.75,-4.25,1),所以变远了。
课后问题:
对于Frustum,我们知道变换完之后远平面和近平面的z是不变的,那中间任意一点的z呢?是会被推向近平面还是推向远平面?
变远。
很奇怪的是数值变的异常大,比如我指认n是-3 f是-5,得到矩阵之后,给定一个中间点(0,1,-4,1)(这里必须是点,也就是w是1,因为向量平移不变),结果是(0,-3,17,-4) ,由于齐次坐标(x/w,y/w,z/w,w/w),所以结果是(0,0.75,-4.25,1),所以变远了。
第五节 光栅化
上节课内容复习
 观测变换
* 视图变换:利用摄影机和物体相对位置不变,摄影机视口内容不变的原理,把摄影机移动到原点 向上+Y,看向-Z,把其它所有内容都和相机一样运动。
* 从三维投影的二维,提到了两类变换,正交和透视。
做完经典的观测变换(把物体都移动到-1,1这个立方体里面)之后,我们需要把物体画在屏幕上。这步叫做光栅化。
观测变换
* 视图变换:利用摄影机和物体相对位置不变,摄影机视口内容不变的原理,把摄影机移动到原点 向上+Y,看向-Z,把其它所有内容都和相机一样运动。
* 从三维投影的二维,提到了两类变换,正交和透视。
做完经典的观测变换(把物体都移动到-1,1这个立方体里面)之后,我们需要把物体画在屏幕上。这步叫做光栅化。
透视投影转换正交投影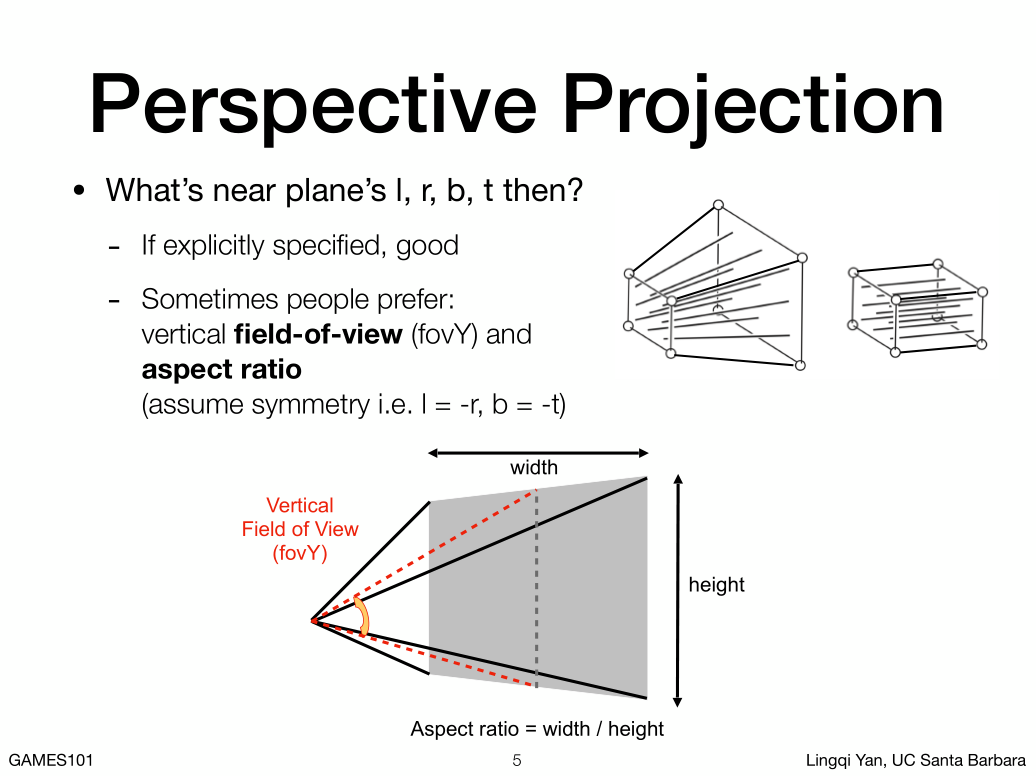
遮挡和可见性
透视投影近平面推导
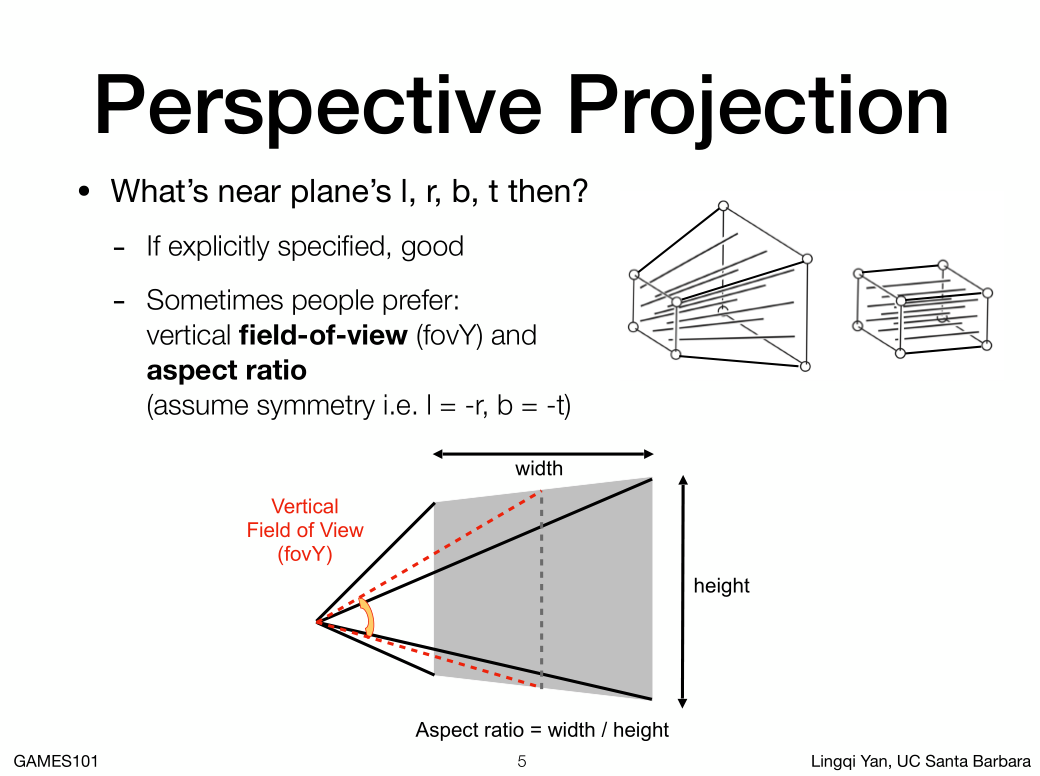 之前我们通过左右(L,R)描述平截头体的近平面。
两个概念:
1. 长宽比
2. 垂直可视角度
垂直可视角度越大越是广角,但是透视投影明显(鱼眼),垂直可视角度越小越是长焦,接近正交投影,透视小。
通过长宽比,我们可以推出垂直可视角度
之前我们通过左右(L,R)描述平截头体的近平面。
两个概念:
1. 长宽比
2. 垂直可视角度
垂直可视角度越大越是广角,但是透视投影明显(鱼眼),垂直可视角度越小越是长焦,接近正交投影,透视小。
通过长宽比,我们可以推出垂直可视角度
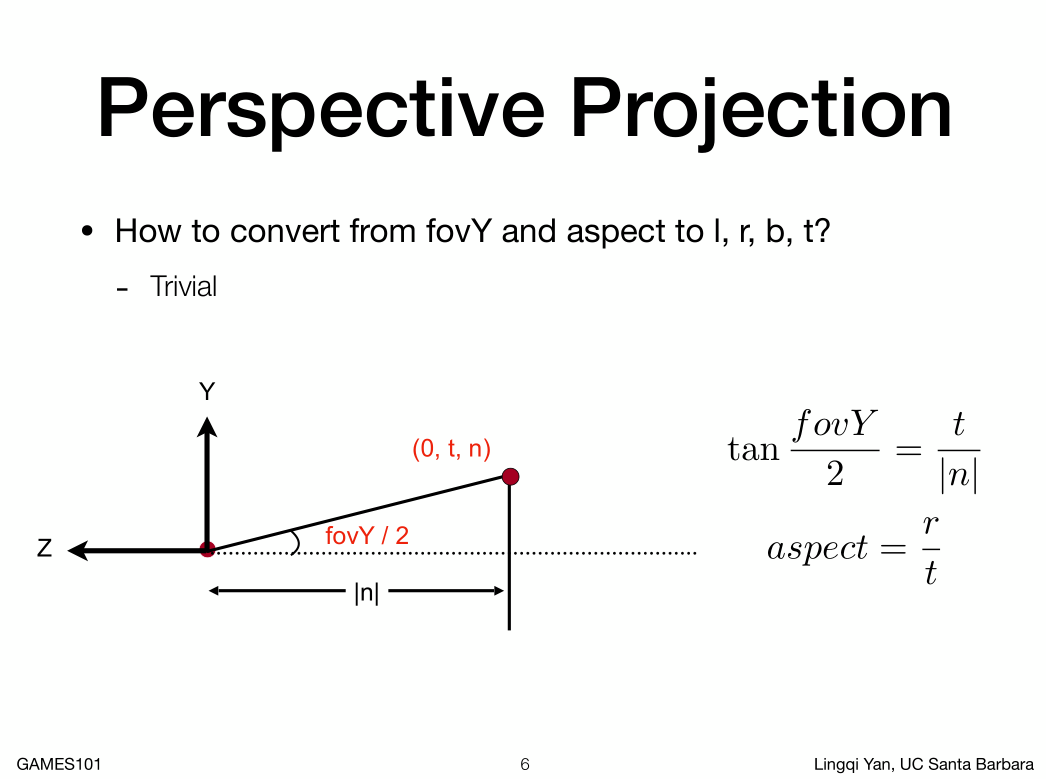 也就是说,只要给定宽高比和垂直可视角度,我们就可以创建一个视锥.
#### 什么是MVP
也就是说,只要给定宽高比和垂直可视角度,我们就可以创建一个视锥.
#### 什么是MVP
 * M
物体自身位移
* V
把摄影机移动到0,0,0 看向-z 头朝正Y,其它物体也和摄影机保持不变,移动到相应位置
* P
正交投影: 先定义一个boudingbox,再把boudingbox变换到(-1,1)3次方空间
透视投影: 平截头体变换到(-1,1)3次方空间
* M
物体自身位移
* V
把摄影机移动到0,0,0 看向-z 头朝正Y,其它物体也和摄影机保持不变,移动到相应位置
* P
正交投影: 先定义一个boudingbox,再把boudingbox变换到(-1,1)3次方空间
透视投影: 平截头体变换到(-1,1)3次方空间
标准立方体空间到屏幕

- 什么是屏幕:
图形学上认为是一个数组,数组里面存储着像素。
数组的大小就是分辨率。
屏幕是一个典型的光栅成像设备。 - 什么是光栅化:
raster == screen in german
rasterize == 再屏幕上绘制 - 什么是像素(一种说法:Pixel是picture element的缩写)
对于这门课简单的抽象理解带颜色的小方块,其实很复杂
RGB组成颜色
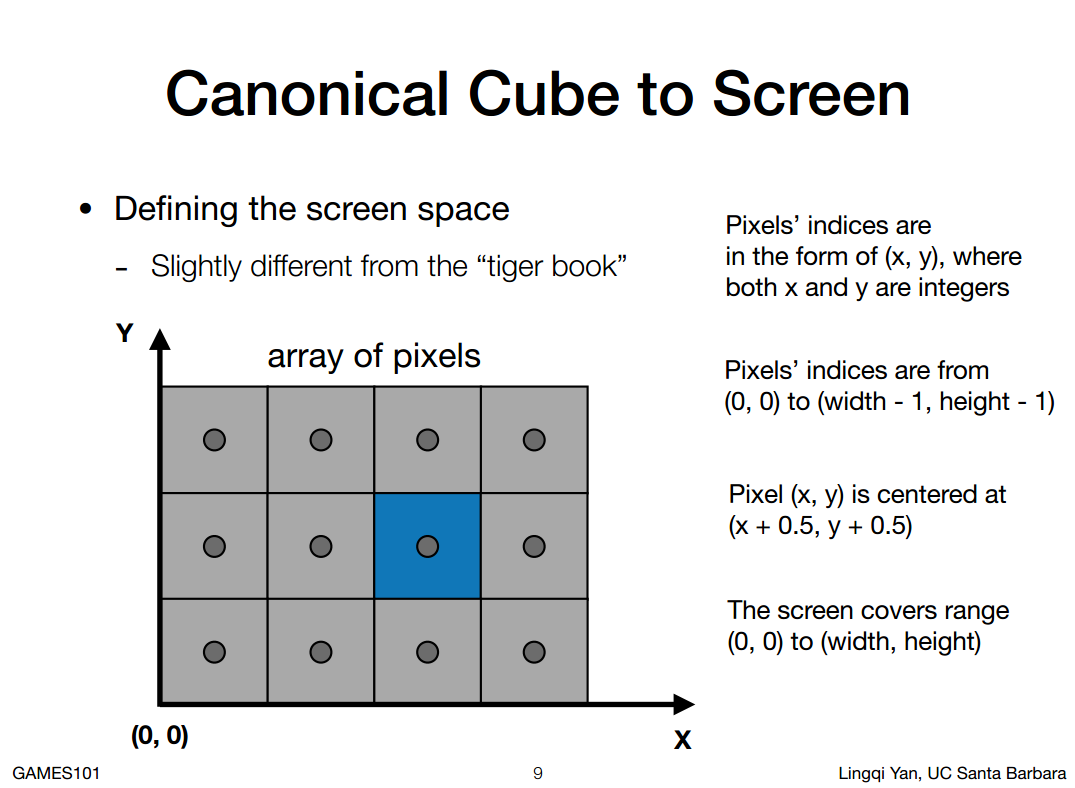 定义屏幕空间
什么是屏幕空间:
相当于在屏幕上建立一个坐标系,左下角是(0,0)。
这样每一个像素都可以用(x,y)表示。
分辨率可以用(0,0)到(width-1,height-1)表示,
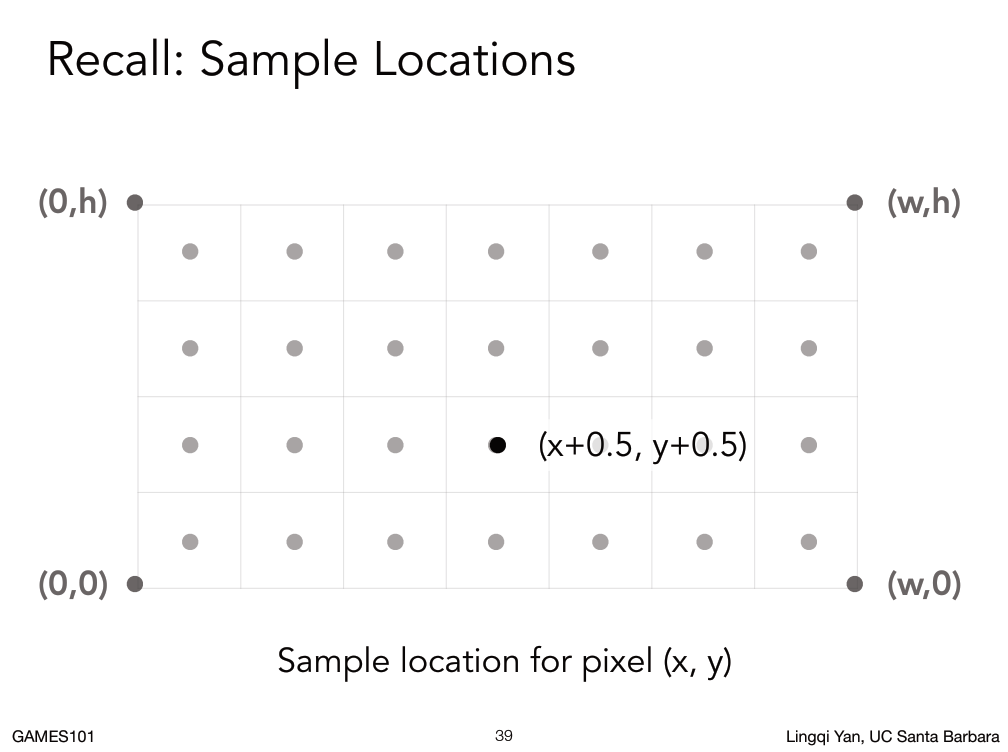
每个像素的中心坐标实际上是(x+0.5,y+0.5)
一个像素会覆盖(1,1)宽度,整个屏幕(0,0)到(width,height)
定义屏幕空间
什么是屏幕空间:
相当于在屏幕上建立一个坐标系,左下角是(0,0)。
这样每一个像素都可以用(x,y)表示。
分辨率可以用(0,0)到(width-1,height-1)表示,
每个像素的中心坐标实际上是(x+0.5,y+0.5)
一个像素会覆盖(1,1)宽度,整个屏幕(0,0)到(width,height)
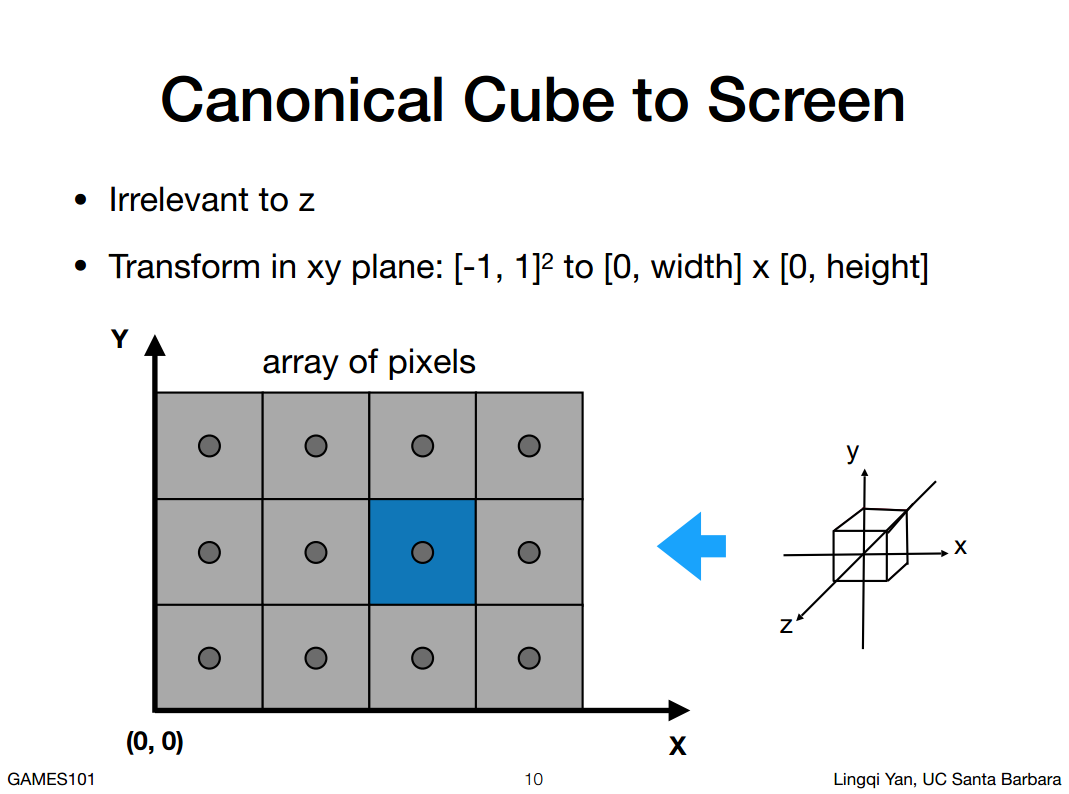
接下来就是把(-1,1)3这个标准空间映射到屏幕上,首先有一个问题就是 xyz 到xy,怎么处理z呢?
先不管它,那就是等于是把xy屏幕(-1,1)2 映射到(0,width)*(0,height),怎么做呢?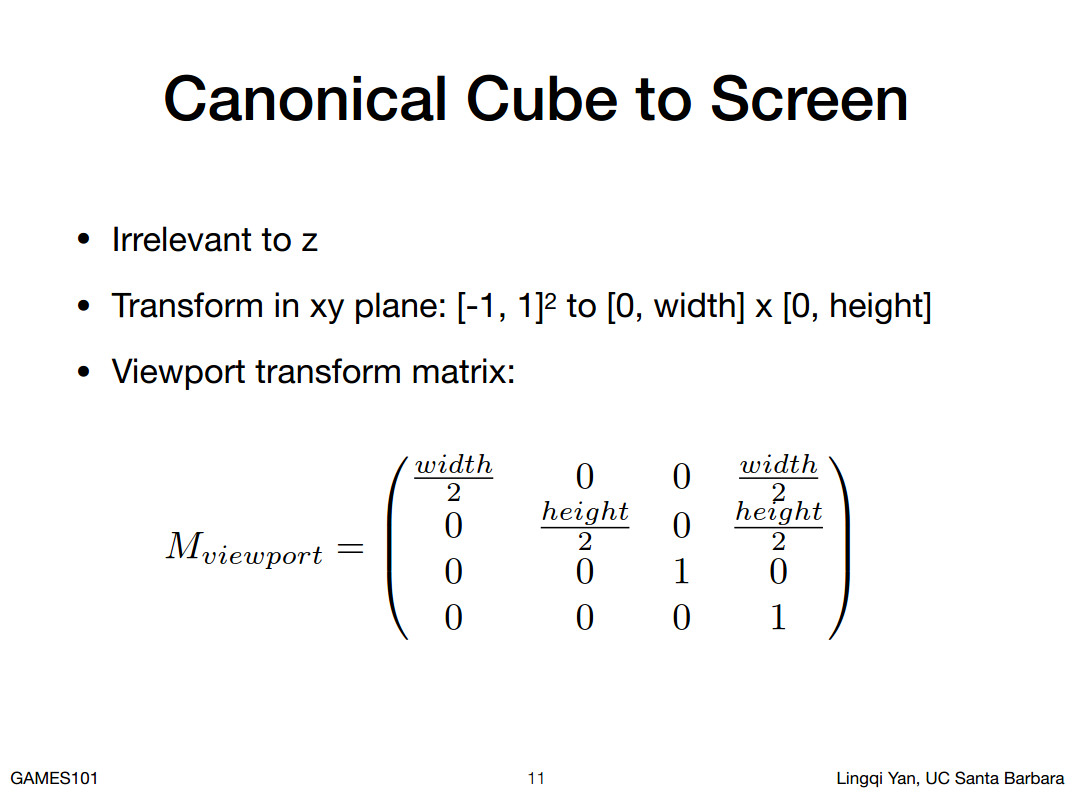
注意这里注意变完之后,中心还在屏幕坐标的中心在左下角,我们要移动中心到屏幕的中心,所以最后一列是有内容的。
光栅化,三角形到像素

几种光栅化显示设备:
- 示波器
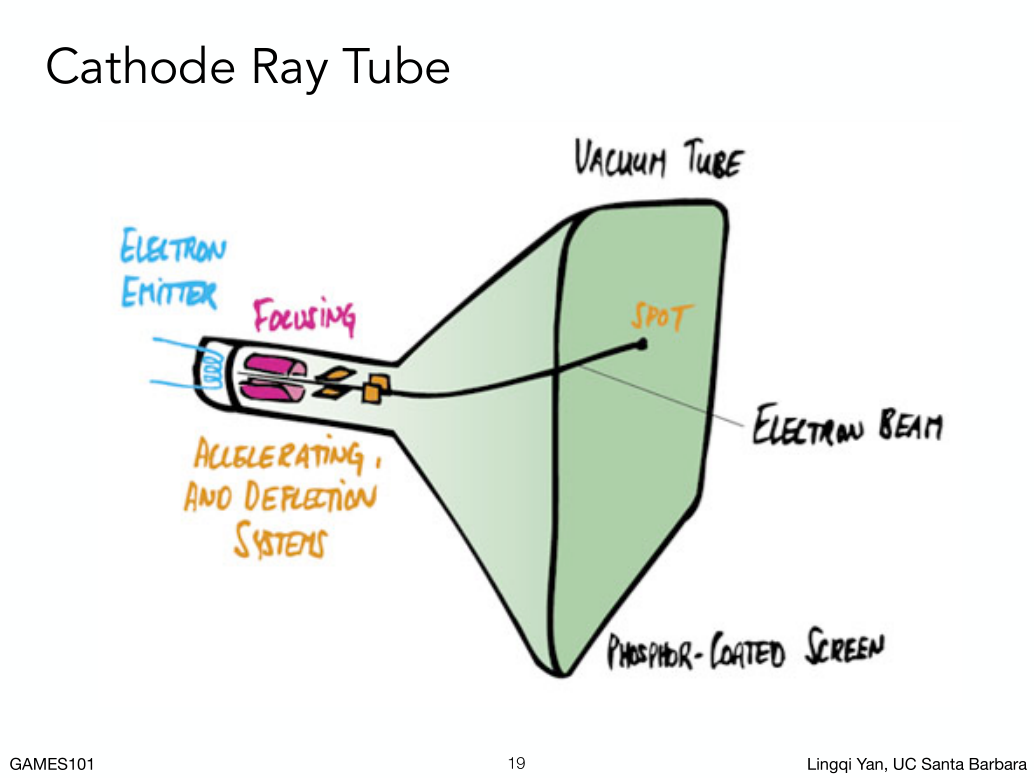
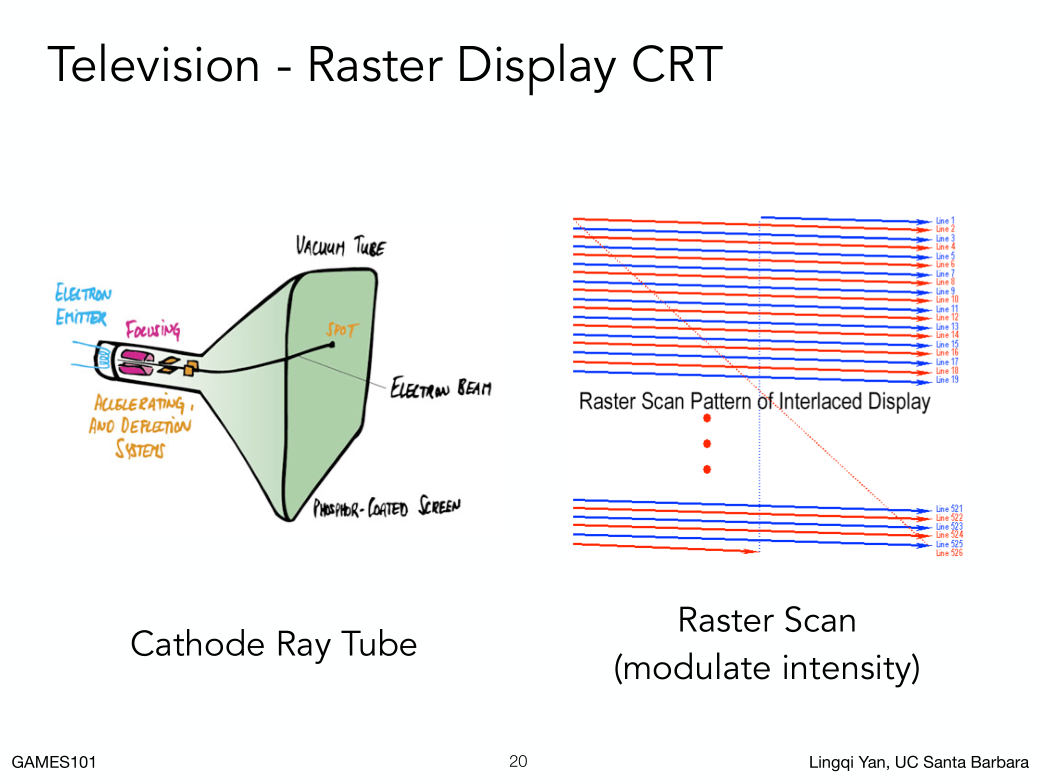 为了使画面刷新快,利用视觉暂留技术,每次只画一半,画完奇数行画偶数行,这种技术叫隔行扫描。
现在在视频压缩里面还有应用。
为了使画面刷新快,利用视觉暂留技术,每次只画一半,画完奇数行画偶数行,这种技术叫隔行扫描。
现在在视频压缩里面还有应用。
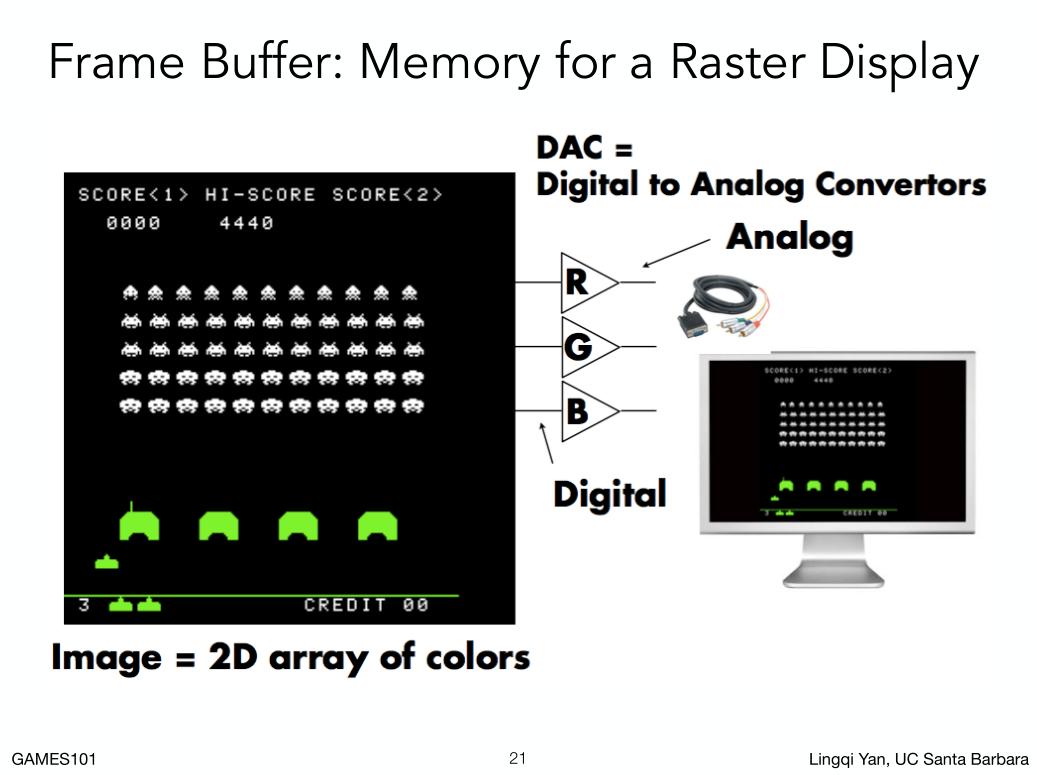 给我一个显示器,我怎么知道他要显示什么呢?通过显存里面的一块区域,把这块区域映射到屏幕上,这里就是现在屏幕的显示方式,我们可以生成不同的图形,存储在不同的显存区域,告诉显示器到底显示哪一幅图。
给我一个显示器,我怎么知道他要显示什么呢?通过显存里面的一块区域,把这块区域映射到屏幕上,这里就是现在屏幕的显示方式,我们可以生成不同的图形,存储在不同的显存区域,告诉显示器到底显示哪一幅图。
 * 平板显示器
低分辨率:计算器
高分辨率:视网膜屏
* 平板显示器
低分辨率:计算器
高分辨率:视网膜屏
 通过液晶的扭曲,改变通过它的光的扭曲水平。
通过液晶的扭曲,改变通过它的光的扭曲水平。
 * 发光二极管
* 发光二极管
 * 电子墨水屏
* 电子墨水屏

为什么是三角形

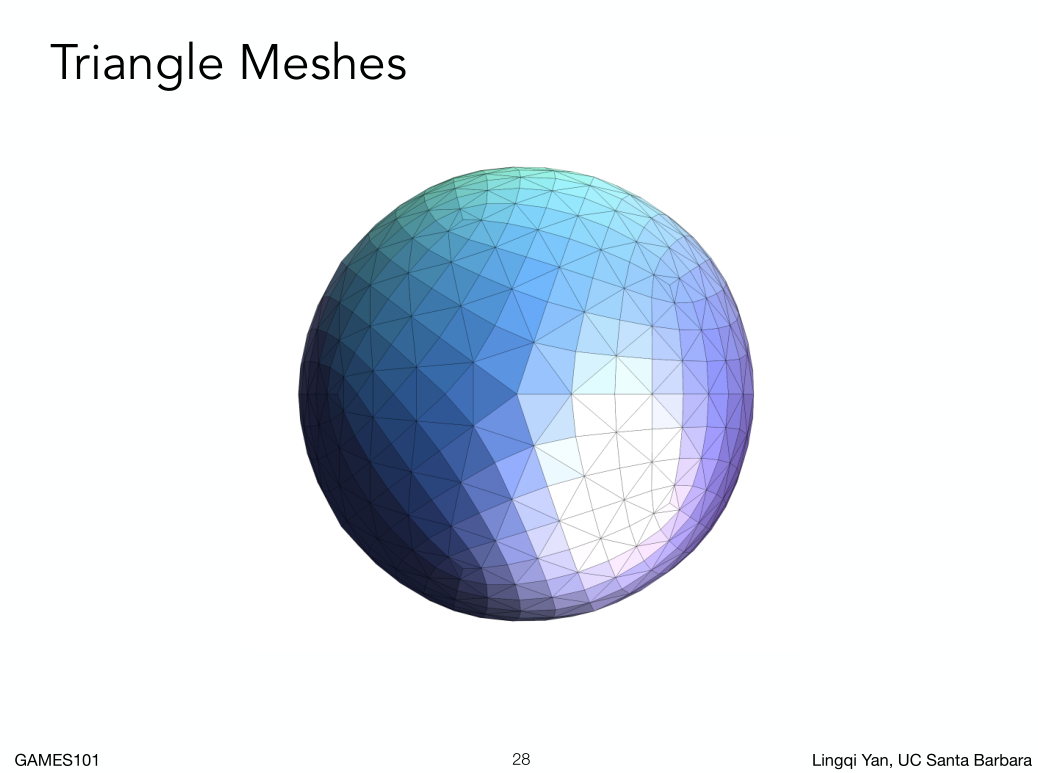

- 最基础的多边形,可以分解任何其它多边形
- 特殊的属性。
- 给定任意三个点,练成三角形都是一个平面。
- 三角形内外定义非常清晰,可以通过向量的叉积判断一个点在不在三角形内。
- 三角形可以定义个插值从一个点到另外俩个点。
如何判断一个像素和三角形的关系
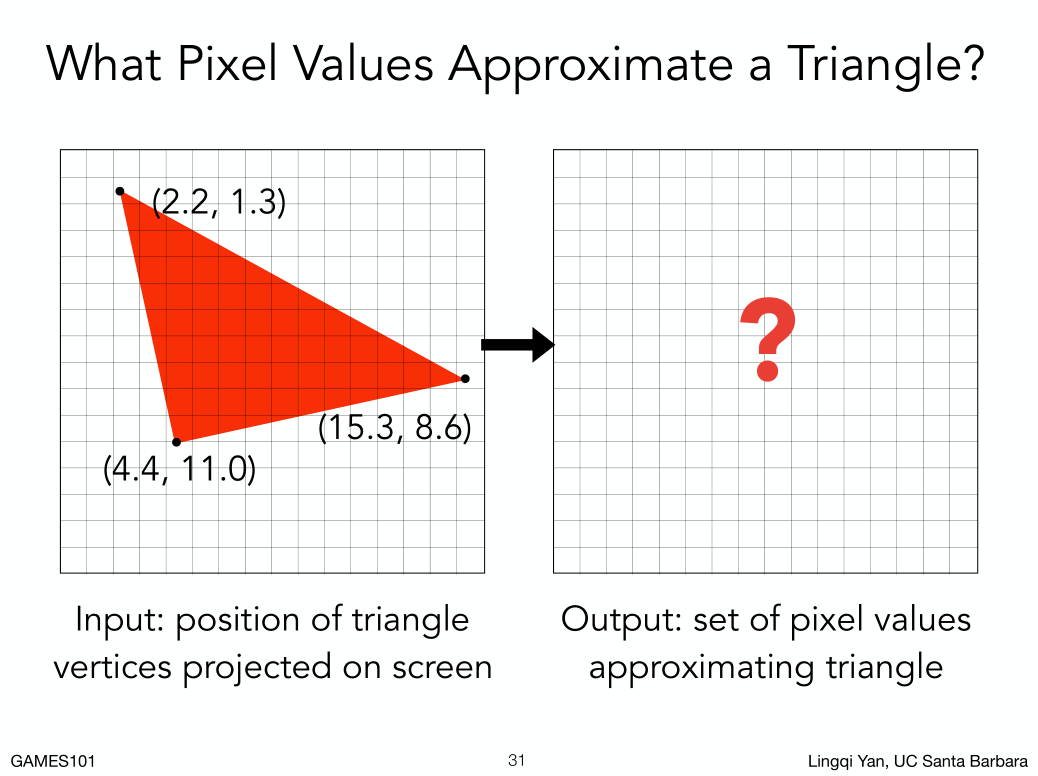 判断一个像素和三角形的位置关系,或者说通过像素的中心点判断和三角形的位置关系。
一个简单的做法:
判断一个像素和三角形的位置关系,或者说通过像素的中心点判断和三角形的位置关系。
一个简单的做法:
 通过采样,
什么是采样:
通过采样,
什么是采样:
 采样就是把一个函数给**离散化**的过程。比如定义一个函数 F(X) = sin(X),然后不停的带入x=1,到x=100,看对应的F(X)的值。
采样是一个非常重要的概念,在图像学里面涉及到各种各样的采样,这里说的采样是指利用像素中心对屏幕空间((0,width)到(0,height))的采样。
后面还要采样 时间 位置 反射,
采样就是把一个函数给**离散化**的过程。比如定义一个函数 F(X) = sin(X),然后不停的带入x=1,到x=100,看对应的F(X)的值。
采样是一个非常重要的概念,在图像学里面涉及到各种各样的采样,这里说的采样是指利用像素中心对屏幕空间((0,width)到(0,height))的采样。
后面还要采样 时间 位置 反射,
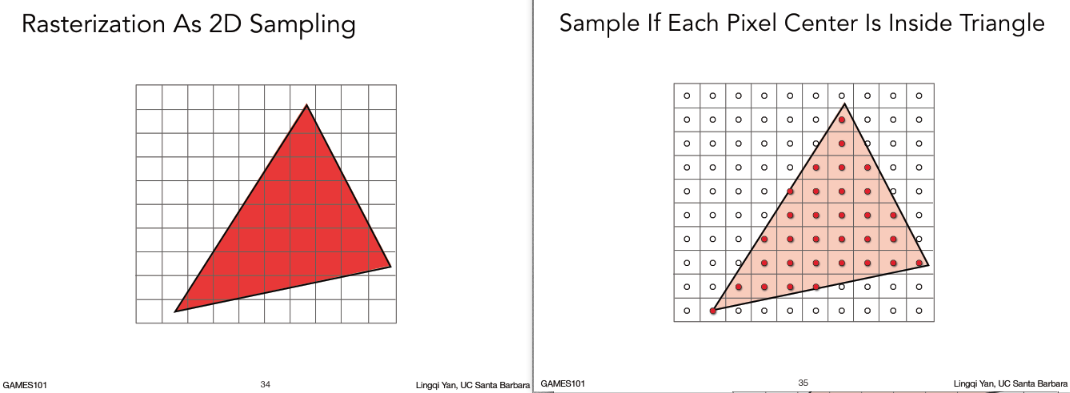
 定义一个函数inside,给你一个三角形,给你屏幕空间的任意一点(x,y)我就知道点是不是在三角形内。
定义一个函数inside,给你一个三角形,给你屏幕空间的任意一点(x,y)我就知道点是不是在三角形内。
 注意这里 inside 返回 0或者1 ,0代表在,1代表不在。
注意这里 inside 返回 0或者1 ,0代表在,1代表不在。
然后就是inside函数是怎么实现的,利用叉积。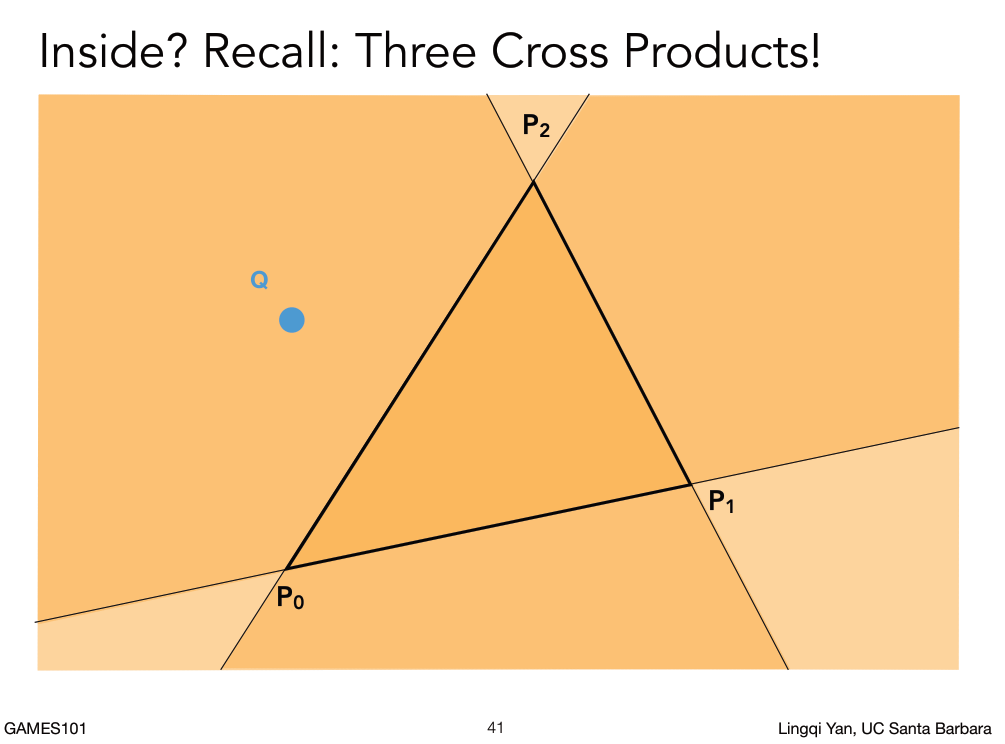
P1P2叉乘P1Q,右手螺旋定则(顺时针),朝屏幕外得到Z正值,左。
P0P1叉乘P0Q,右手螺旋定则(顺时针),朝屏幕外得到Z正值,左。
p2p0叉乘P2Q,右手螺旋定则(逆时针),朝屏幕里得到Z负值,右。
只有全是正或者全是负才是三角形内部,所以Q所以不在三角形内部。
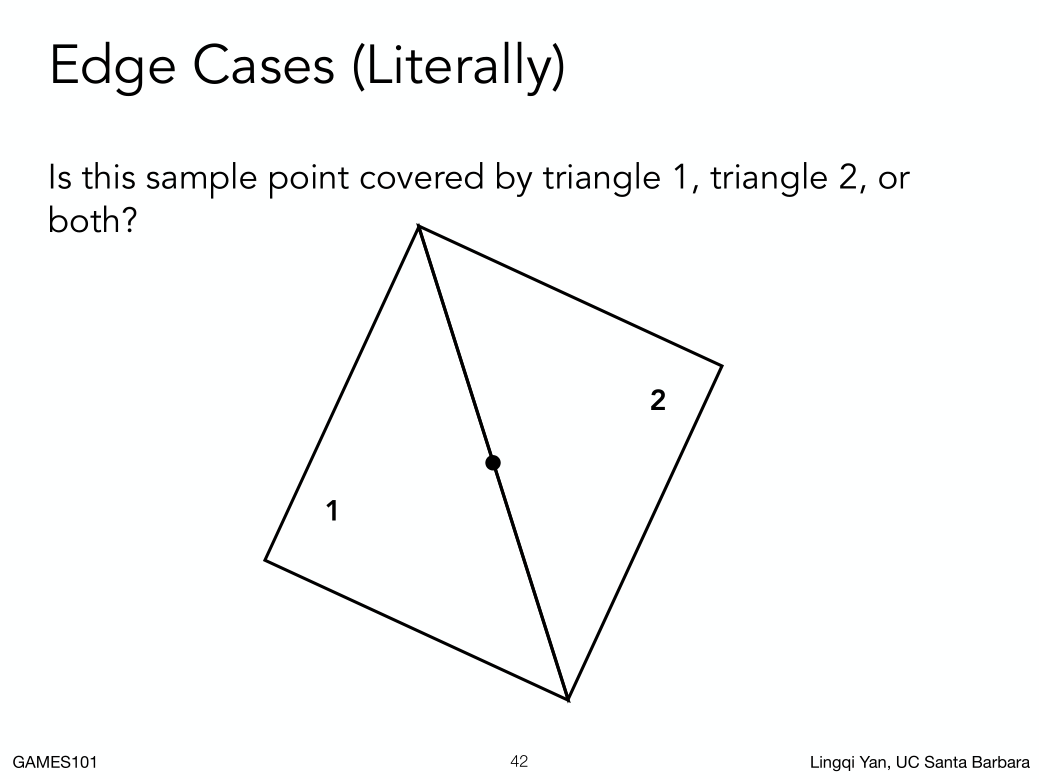 如果碰巧在三角形的边界,该怎么处理呢?在图形学里面要么不做处理,要么特殊处理,这门课不做处理。自己定义一个标准即可。
在dx和opengl的api里面定义非常严格,点落在上边和左边算内部,落在右边和下边不算在内部。
如果碰巧在三角形的边界,该怎么处理呢?在图形学里面要么不做处理,要么特殊处理,这门课不做处理。自己定义一个标准即可。
在dx和opengl的api里面定义非常严格,点落在上边和左边算内部,落在右边和下边不算在内部。
 一个三角形相对于屏幕上很多像素点其实很小,如果把全部的像素点都测试一下的话慢而且没必要,就像白色那条像素一样,可以只测试这个三角形Bounding Box内的像素(蓝色区域),怎么计算这个Bounding Box呢?取P2 P1 P0这三个点的X最大和最小,Y最大最小,有了这四个数就可以得到一个矩形空间。
一个三角形相对于屏幕上很多像素点其实很小,如果把全部的像素点都测试一下的话慢而且没必要,就像白色那条像素一样,可以只测试这个三角形Bounding Box内的像素(蓝色区域),怎么计算这个Bounding Box呢?取P2 P1 P0这三个点的X最大和最小,Y最大最小,有了这四个数就可以得到一个矩形空间。
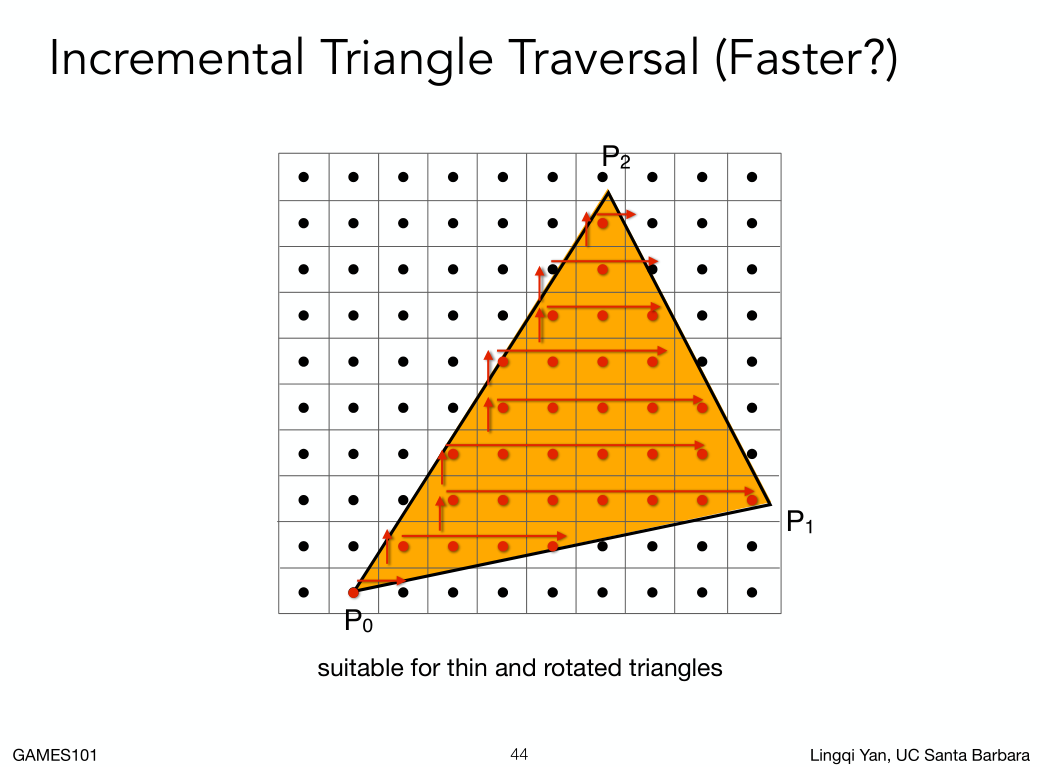 还可以每一行都找一下Bounding Box。
还可以每一行都找一下Bounding Box。
实际屏幕的光栅化

 注意打印是减色模式。
注意打印是减色模式。

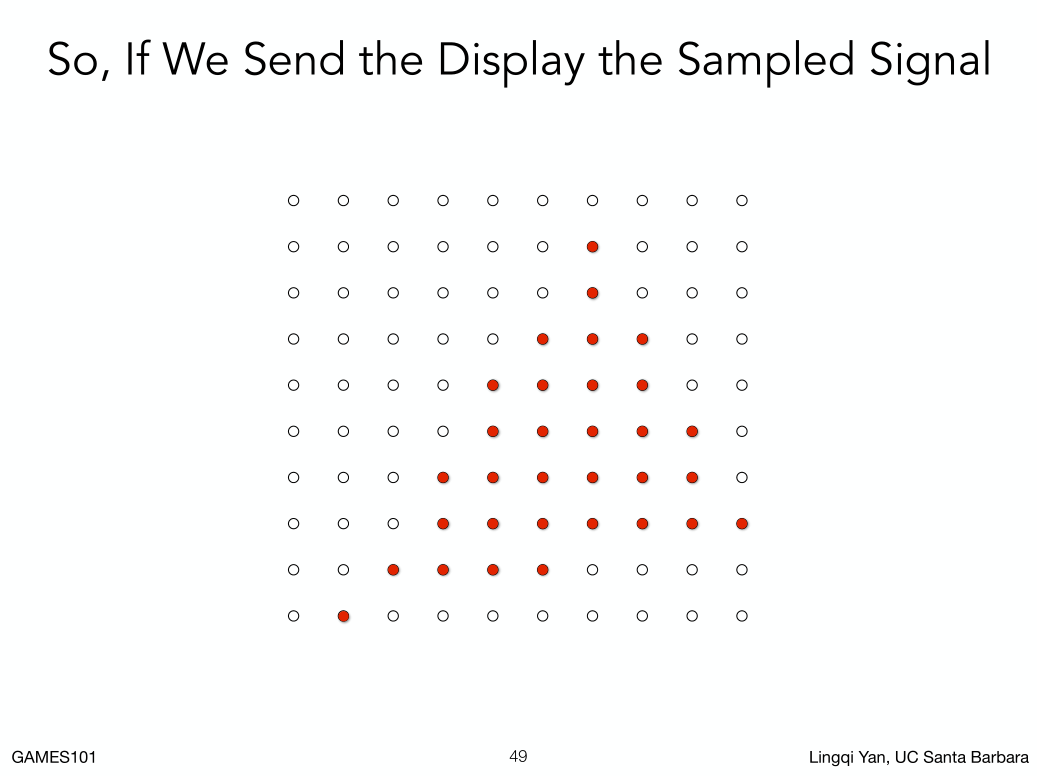
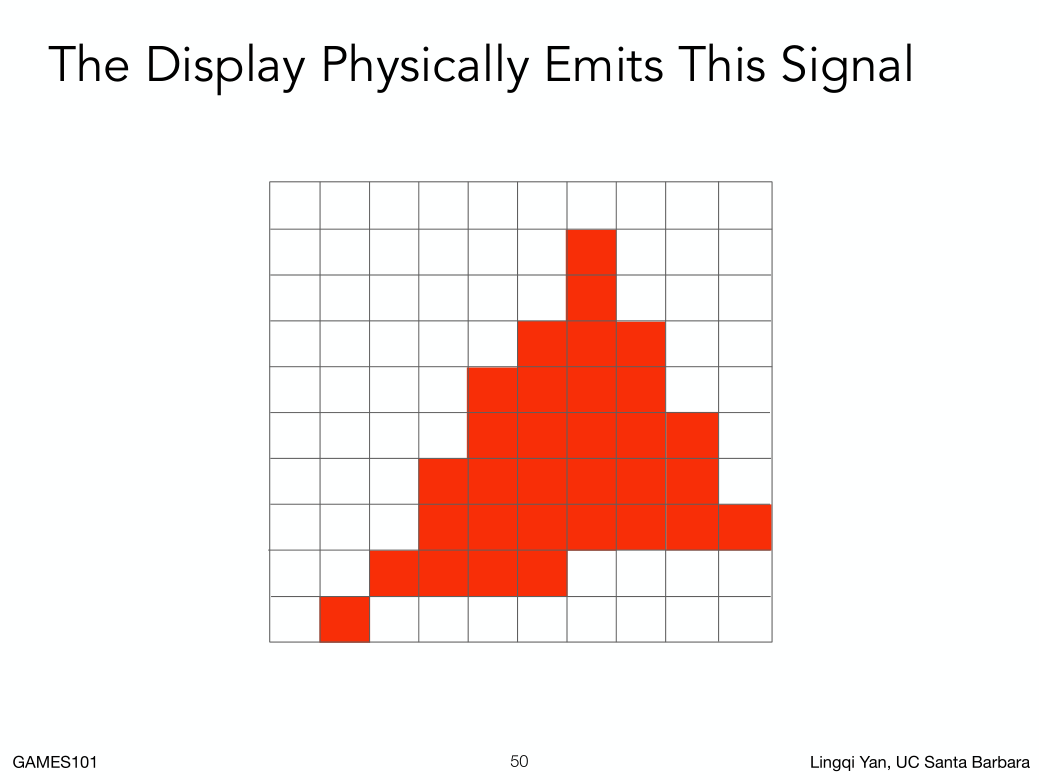
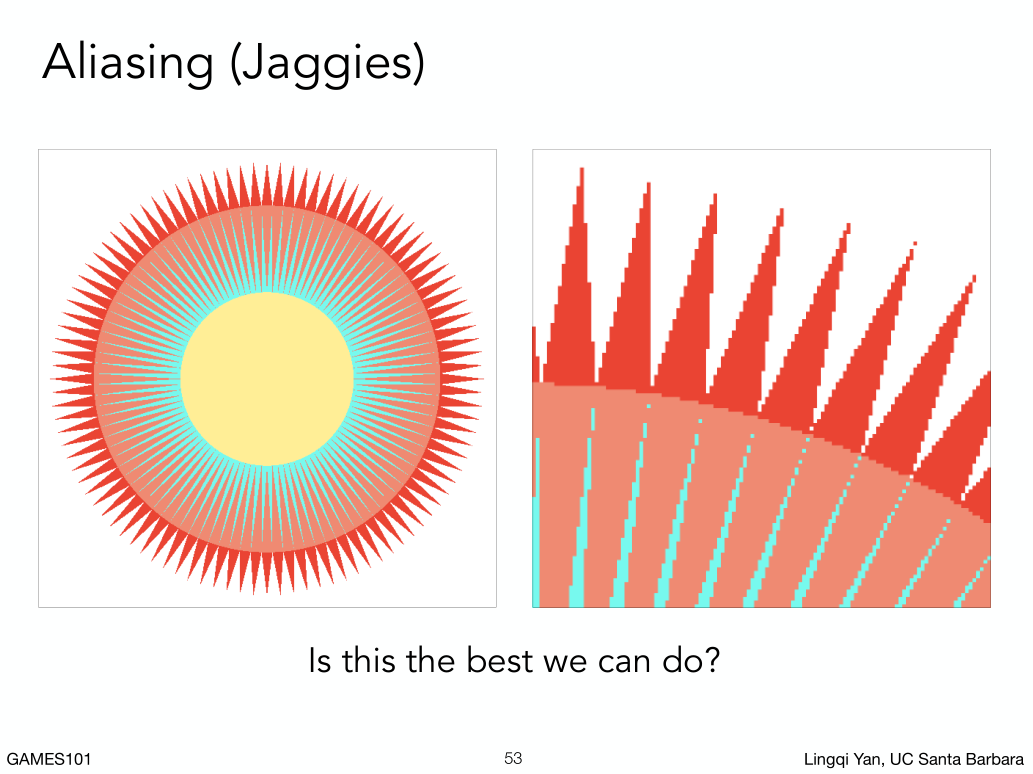
 锯齿是光栅化一直在致力解决的问题。
锯齿是光栅化一直在致力解决的问题。
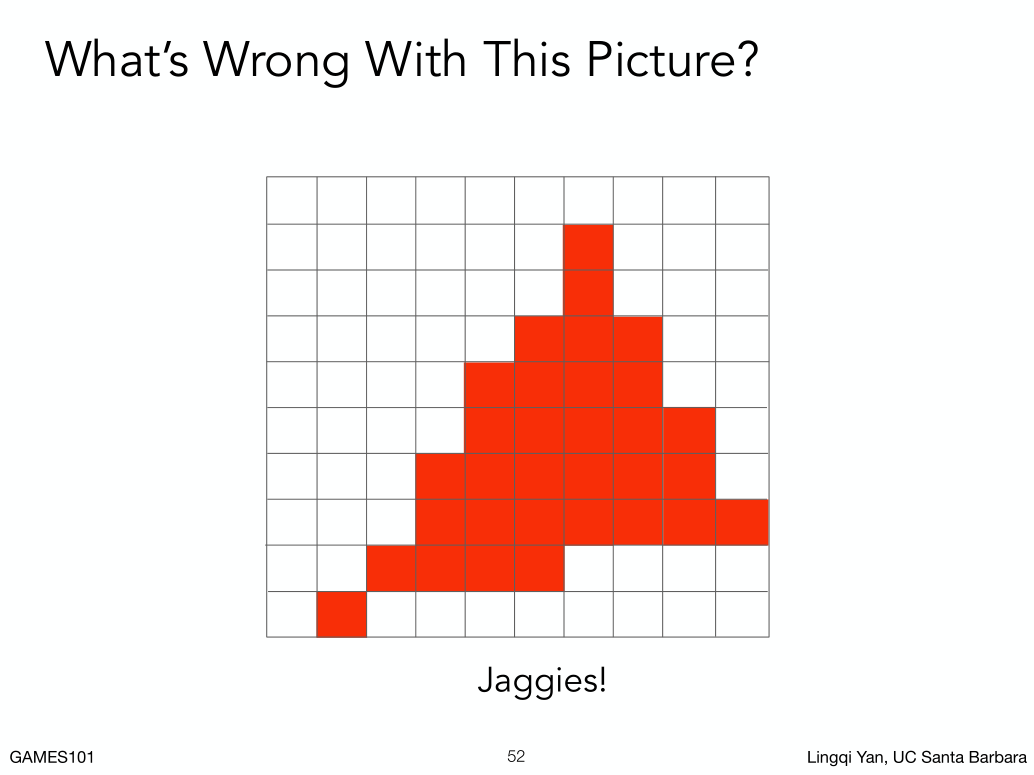 有锯齿就有抗锯齿。
有锯齿就有抗锯齿。